搜索
【题目】如图，丁轩同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行20m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知丁轩同学的身高是1.5m，两个路灯的高度都是9m，则两路灯之间的距离是（ ）
A. 24m B. 25m C. 28m D. 30m
参考答案：
【答案】D
【解析】由题意可得:EP∥BD,所以△AEP∽△ADB,所以
,因为EP=1.5,BD=9,所以
,解得:AP=5,因为AP=BQ,PQ=20,所以AB=AP+BQ+PQ=5+5+20=30,故选D.
点睛:本题主要考查相似三角形的对应边成比例在解决实际问题中的应用,应用相似三角形可以间接地计算一些不易直接测量的物体的高度和宽度,解题时关键是找出相似三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）．
（1）写出点A、B的坐标:
（2）将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A′B′C′，画出△A′B′C′；
（3）若AB边上有一点M（a，b），平移后对应的点M′的坐标为:
（4）求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解2018届本科生的就业情况，某网站对2018届本科生的签约状况进行了网络调查，至4月底，参与网络调查的12000人中，只有4320人已与用人单位签约在这个调查中，样本容量是__________．
-
科目： 来源： 题型：
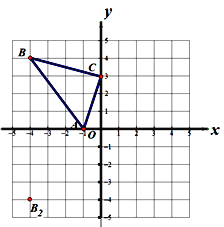
查看答案和解析>>【题目】如图所示，在直角坐标系xOy中，△ABC三点的坐标分别为A(－l，0)，B(－4，4)，C(0，3)．
（1）在图中画出△ABC关于y轴对称的图形△A1B1C1；写出B1的坐标为___________.
（2）填空：在图中，若B2(－4，－4)与点B关于一条直线成轴对称，则这条对称轴是________，此时点C关于这条直线的对称点C2的坐标为_____________；
（3）在y轴上确定一点P，使△APB的周长最小.(注：简要说明作法，保留作图痕迹，不求坐标)
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究归纳题：
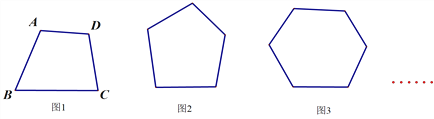
(1)试验分析：
如图1，经过A点可以做__________条对角线；同样，经过B点可以做__________条；经过C点可以做__________条；经过D点可以做__________条对角线.
通过以上分析和总结，图1共有___________条对角线.
（2）拓展延伸：
运用（1）的分析方法，可得：
图2共有_____________条对角线；
图3共有_____________条对角线；
(3)探索归纳：
对于n边形(n>3)，共有_____________条对角线．(用含n的式子表示)
(4)特例验证：
十边形有__________________对角线.
-
科目： 来源： 题型：
查看答案和解析>>【题目】用小立方体搭一个几何体，使它的主视图和俯视图如图所示，俯视图中小正方形中字母表示在该位置小立方体的个数，请解答下列问题：
(1)a＝ ，b＝ ，c＝ ；
(2)这个几何体最少由 个小立方体搭成，最多由 个小立方体搭成；
(3)当d＝2，e＝1，f＝2时，画出这个几何体的左视图．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列语句，是真命题的是( )
A.对顶角相等B.同位角相等C.内错角相等D.同旁内角互补
相关试题
