【题目】求证:角平分线和中线重合的三角形是等腰三角形.
参考答案:
【答案】见解析
【解析】
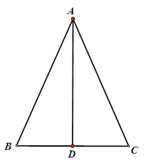
作出图形,延长AD到E,使DE=AD,连接BE,先证明△ADC和△EBD全等,根据全等三角形对应边相等得到AC=BE,对应角相等得到∠E=∠CAD,又中线也是角平分线,可以再证出AB=BE,从而证明AB=AC,所以是等腰三角形.
已知.在△ABC中,BD=CD,AD平分∠BAC.
求证:AB=AC.
证明:如图,延长AD到E,使DE=AD,连接BE.
∵AD是中线,∴BD=CD.在△ADC和△EBD中,∵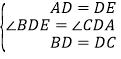 ,∴△ADC≌△EBD(SAS),∴BE=AC,∠E=∠CAD.
,∴△ADC≌△EBD(SAS),∴BE=AC,∠E=∠CAD.
∵AD是角平分线,∴∠CAD=∠BAD,∴∠E=∠BAD,∴AB=BE,∴AB=AC,∴△ABC是等腰三角形.
即:角平分线和中线重合的三角形是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程交由甲、乙两个工程队来完成,已知甲工程队单独完成需要60天,乙工程队单独完成需要40天
(1)若甲工程队先做30天后,剩余由乙工程队来完成,还需要用时 天
(2)若甲工程队先做20天,乙工程队再参加,两个工程队一起来完成剩余的工程,求共需多少天完成该工程任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
 中,
中, ,垂足为点H,若
,垂足为点H,若 ,
, ,则
,则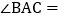 ______
______
-
科目: 来源: 题型:
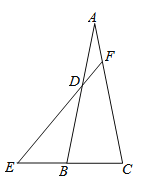
查看答案和解析>>【题目】如图,△ABC是等腰三角形,AB=AC=3,BC=1.点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,开设了体育活动小组,并计划购买一些篮球和排球
 已知每个篮球的售价比每个排球的售价多20元,用1100元购进的篮球数量是用450元购进排球数量的2倍.
已知每个篮球的售价比每个排球的售价多20元,用1100元购进的篮球数量是用450元购进排球数量的2倍. 求每个篮球和每个排球的单价各是多少元;
求每个篮球和每个排球的单价各是多少元; 若学校计划购进篮球和排球共50个,且购进的总费用不超过4900元,则学校最多可以购进篮球多少个?
若学校计划购进篮球和排球共50个,且购进的总费用不超过4900元,则学校最多可以购进篮球多少个?
相关试题

