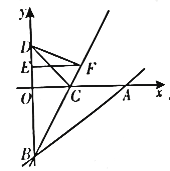
【题目】如图,在平面直角坐标系xOy中,直线![]() 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将![]() 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当![]() PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。
(3)在坐标轴上是否存在一点H,使得![]() HAB和
HAB和![]() ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
参考答案:
【答案】(1)![]() ;(2)P(
;(2)P(![]() );(3)存在这样的H点使之成立;
);(3)存在这样的H点使之成立;![]() ,
,![]() ,
,![]()
【解析】
(1)根据翻折求出点A的坐标,代入即可求得;
(2)求出直线AE和直线BC的解析式,联立可求出点P的坐标;
(3)分两种情况,当点H在x轴上和在y轴上分析.
(1) 对于直线![]() ,
,
当x=0时,y=-6,
又∵D(0,4),
∴BD=10,
由翻折知AB=BD=10,
根据勾股定理得OA=![]() =
=![]() =8,
=8,
∴A(8,0),
把A(8,0)代入![]() 得k=
得k=![]() ,
,
∴y=![]()
(2)过点D作BC的对称点A(8,0),
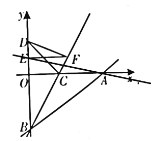
∵E(0,3) ,
∴直线AE的解析式为y=-![]() x+3,
x+3,
∵A,D关于BC对称,
∴OP=OP,![]() PDE的周长=DE+DP+EP,
PDE的周长=DE+DP+EP,
设OC=x,则CD=CA=8-x,
在Rt△DOC中,x+4=(8-x),解得x=3,
∴C(3,0)
∵C(3,0),B(0,-6),
∴直线BC的解析式为y=2x-6,
联立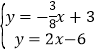 ,解得
,解得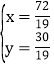 ,
,
∴P(![]() );
);
(3) 存在这样的H点使之成立,
∵![]() =
=![]() ×AC×BO=
×AC×BO=![]() ×5×6=15,
×5×6=15,
∴当点H在x轴上时,得![]() ;
;
当点H在y轴上时,设H(0,a),
∵![]() =
=![]() ∣a+6∣·8=15,即a=-
∣a+6∣·8=15,即a=-![]() 或-
或-![]() ,
,
∴综上,![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】林华在2018年共两次到某商场按照标价购买了A,B两种商品,其购买情况如下表:
购买A商品的数量(个)
购买B商品的数量(个)
购买两种商品的总费用(元)
第一次购买
6
5
1140
第二次购买
3
7
1110
(1)分别求出A、B两种商品的标价。
(2)最近商场实行“迎2019新春”的促销活动,A,B两种商品都打折且折扣数相同,于是林华前往商场花1062元又购买了9个A商品和8个B商品,试问本次促销活动中A,B商品的折扣数都为多少?在本次购买中,林华共节约了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和 都是等边三角形,连接AC,DE,CD.
都是等边三角形,连接AC,DE,CD.(1)猜想AC与DE的数量关系,并说明理由。
(2)给出定义:若一个四边形中存在一组邻边的平方等于一条对角线的平方,则这个四边形为勾股四边形.如图,若
 ,求证:四边形ABCD是勾股四边形。
,求证:四边形ABCD是勾股四边形。(3)设
 ,
, ,
, 的面积分别是
的面积分别是 ,若
,若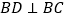 ,试探究
,试探究 与
与 之间满足的等量关系。
之间满足的等量关系。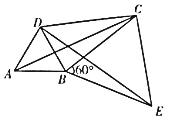
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 .
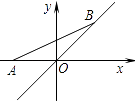
-
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
相关试题

