【题目】林华在2018年共两次到某商场按照标价购买了A,B两种商品,其购买情况如下表:
购买A商品的数量(个) | 购买B商品的数量(个) | 购买两种商品的总费用(元) | |
第一次购买 | 6 | 5 | 1140 |
第二次购买 | 3 | 7 | 1110 |
(1)分别求出A、B两种商品的标价。
(2)最近商场实行“迎2019新春”的促销活动,A,B两种商品都打折且折扣数相同,于是林华前往商场花1062元又购买了9个A商品和8个B商品,试问本次促销活动中A,B商品的折扣数都为多少?在本次购买中,林华共节约了多少钱?
参考答案:
【答案】(1)A种商品标价90元,B种商品标价120元;(2)两种商品打6折出售,共节约708元
【解析】
(1)设商品A的标价为x元/个,商品B的标价为y元/个,根据总价=单价×数量结合前两次购买商品的数量及费用,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据折扣率=现价÷原价×10,即可求出结论.
(1)设A种商品标价x元,B种商品标价y元,则
![]() ,
,
解得![]() .
.
∴A种商品标价90元,B种商品标价120元;
(2)设商店是打a折出售的这两种产品,根据题意得
(9×90+8×120) ×![]() =1062,
=1062,
解得a=6,
故商店是打6折出售的这两种产品.
林华节省了9×90+8×120-1062=708(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,与抛物线交于点D,若OA=1,CD=4,则线段AB的长为( )
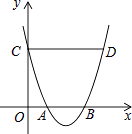
A.2
B.1
C.3
D.1.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为 .
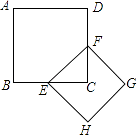
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和 都是等边三角形,连接AC,DE,CD.
都是等边三角形,连接AC,DE,CD.(1)猜想AC与DE的数量关系,并说明理由。
(2)给出定义:若一个四边形中存在一组邻边的平方等于一条对角线的平方,则这个四边形为勾股四边形.如图,若
 ,求证:四边形ABCD是勾股四边形。
,求证:四边形ABCD是勾股四边形。(3)设
 ,
, ,
,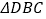 的面积分别是
的面积分别是 ,若
,若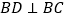 ,试探究
,试探究 与
与 之间满足的等量关系。
之间满足的等量关系。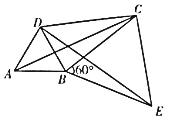
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
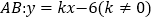 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当
 PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。(3)在坐标轴上是否存在一点H,使得
 HAB和
HAB和 ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。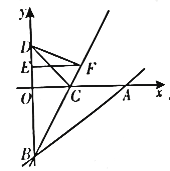
相关试题

