【题目】如图,点A的坐标为(﹣1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 . 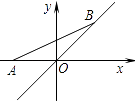
参考答案:
【答案】(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】解:先过点A作AB′⊥OB,垂足为点B′,
由垂线段最短可知,当B′与点B重合时AB最短,
∵点B在直线y=x上运动,
∴△AOB′是等腰直角三角形,
过B′作B′C⊥x轴,垂足为C,
∴△B′CO为等腰直角三角形,
∵点A的坐标为(﹣1,0),
∴OC=CB′= ![]() OA=
OA= ![]() ×1=
×1= ![]() ,
,
∴B′坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),
),
即当线段AB最短时,点B的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).
).
故答案为:(﹣ ![]() ,﹣
,﹣ ![]() ).
).
先过点A作AB′⊥OB,垂足为点B′,由于点B在直线y=x上运动,所以△AOB′是等腰直角三角形,由勾股定理求出OB′的长即可得出点B′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和 都是等边三角形,连接AC,DE,CD.
都是等边三角形,连接AC,DE,CD.(1)猜想AC与DE的数量关系,并说明理由。
(2)给出定义:若一个四边形中存在一组邻边的平方等于一条对角线的平方,则这个四边形为勾股四边形.如图,若
 ,求证:四边形ABCD是勾股四边形。
,求证:四边形ABCD是勾股四边形。(3)设
 ,
, ,
,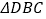 的面积分别是
的面积分别是 ,若
,若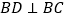 ,试探究
,试探究 与
与 之间满足的等量关系。
之间满足的等量关系。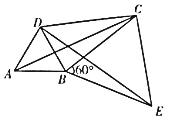
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
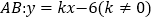 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将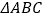 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当
 PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。(3)在坐标轴上是否存在一点H,使得
 HAB和
HAB和 ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。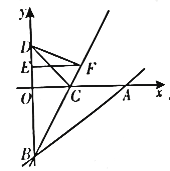
-
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树状图或列表法中的一种列举出这辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
相关试题

