【题目】(1)如图,正方形![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() .求证:
.求证:![]() .
.

(2)如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 在边
在边![]() 上,且
上,且![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)证△ADG≌△ABE,△FAE≌△FAG,根据全等三角形的性质求出即可;
(2)过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.通过证明△ABM≌△ACE(SAS)推知全等三角形的对应边AM=AE、对应角∠BAM=∠CAE;然后由等腰直角三角形的性质和∠MAN=45°得到∠MAN=∠EAN=45°,所以△MAN≌△EAN(SAS),故全等三角形的对应边MN=EN;最后由勾股定理得到EN2=EC2+NC2即MN2=BM2+NC2.
(1)证明:在正方形![]() 中,
中,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,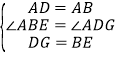 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,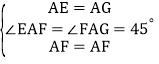 ,
,
![]() ,
,
![]() ;
;
(2)如图,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,截取
,截取![]() ,使
,使![]() .连接
.连接![]() 、
、![]() ,
,
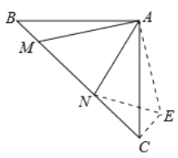
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
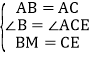 ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
于是,由![]() ,得
,得![]() ,
,
在![]() 和
和![]() 中,
中,
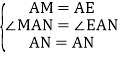 ,
,
![]() ,
,
![]() ,
,
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点P
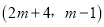 ,试分别根据下列条件,求出点P的坐标:
,试分别根据下列条件,求出点P的坐标:(1)点P在
 轴上;
轴上;(2)点P的纵坐标比横坐标大3;
(3)点P到两坐标的距离相等;
(4)点P在过A(2,-5)点,且与
 轴平行的直线上。
轴平行的直线上。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A逆时针旋转80°后得到△A′B′C′(点B的对应点是点B′,点C的对应点是点C′,连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
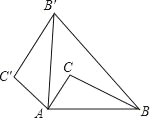
A. 82° B. 80° C. 78° D. 76°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,tanB=
 ,AB=10,AC=2
,AB=10,AC=2 ,将线段AB绕点A旋转到AD,使AD∥BC,连接CD,则CD=_____.
,将线段AB绕点A旋转到AD,使AD∥BC,连接CD,则CD=_____.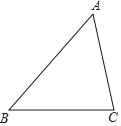
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ACD中,∠B=∠D,tanB=
 ,BC=5,CD=3,∠BCA=90°﹣
,BC=5,CD=3,∠BCA=90°﹣ ∠BCD,则AD=_____.
∠BCD,则AD=_____.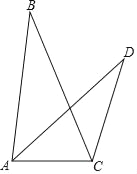
-
科目: 来源: 题型:
查看答案和解析>>【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BAE+∠DCE=∠AEC;
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠BAE+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③,若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG=______°.
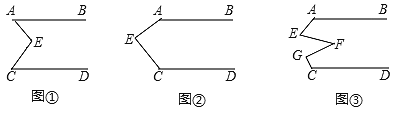
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF是Rt△ABC的中位线,∠BAC=90°,AD是斜边BC边上的中线,EF和AD相交于点O,则下列结论不正确的是( )
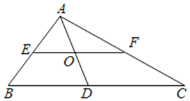
A. AO=ODB. EF=ADC. S△AEO=S△AOFD. S△ABC=2S△AEF
相关试题

