【题目】如图,EF是Rt△ABC的中位线,∠BAC=90°,AD是斜边BC边上的中线,EF和AD相交于点O,则下列结论不正确的是( )
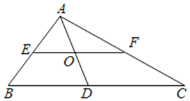
A. AO=ODB. EF=ADC. S△AEO=S△AOFD. S△ABC=2S△AEF
参考答案:
【答案】D
【解析】
根据三角形中位线定理以及直角三角形斜边上的中线等于斜边的一半逐项分析即可.
解:
∵EF是Rt△ABC的中位线,
∴EF![]()
![]() BC ,
BC ,
∵AD是斜边BC边上的中线,
∴AD=![]() BC,
BC,
∴EF=AD,故选项B正确;
∵AE=BE,EO∥BD,
∴AO=OD,故选项A正确;
∵E,O,F,分别是AB,AD,AC中点,
∴EO=![]() BD,OF=
BD,OF=![]() DC,
DC,
∵BD=CD,
∴OE=OF,
又∵EF∥BC,
∴S△AEO=S△AOF,故选项C正确;
∵EF∥BC,
∴△ABC∽△AEF,
∵EF是Rt△ABC的中位线,
∴S△ABC:S△AEF=4:1,
即S△ABC=4S△AEF≠2S△AEF,故选D错误,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,正方形
 中,点
中,点 ,
, 分别在边
分别在边 ,
, 上,
上, ,延长
,延长 到点
到点 ,使
,使 ,连结
,连结 ,
,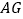 .求证:
.求证: .
.
(2)如图,等腰直角三角形
 中,
中, ,
, ,点
,点 ,
, 在边
在边 上,且
上,且 ,若
,若 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ACD中,∠B=∠D,tanB=
 ,BC=5,CD=3,∠BCA=90°﹣
,BC=5,CD=3,∠BCA=90°﹣ ∠BCD,则AD=_____.
∠BCD,则AD=_____.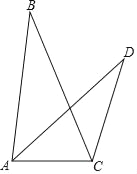
-
科目: 来源: 题型:
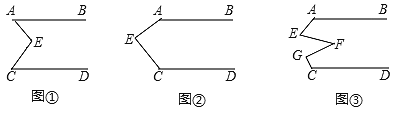
查看答案和解析>>【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BAE+∠DCE=∠AEC;
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠BAE+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③,若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG=______°.
-
科目: 来源: 题型:
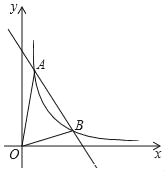
查看答案和解析>>【题目】如图一次函数y=kx+b与反比例函数y=
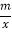 (x>0)的图象交于A(1,6),B(n,2)两点.
(x>0)的图象交于A(1,6),B(n,2)两点.(1)求一次函数和反比例函数的解析式
(2)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,健民体育活动中心从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据健民体育活动中心消费者的需求量,活动中心决定用不超过2550元钱购进甲、乙两种羽毛球共50筒,那么最多可以购进多少筒甲种羽毛球?
相关试题

