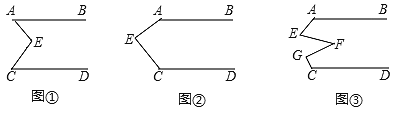
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BAE+∠DCE=∠AEC;
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠BAE+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③,若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG=______°.
参考答案:
【答案】【感知】见解析;【探究】∠BAE+∠AEC+∠DCE=360°;【应用】396°.
【解析】
感知:如图①,过点E作EF∥AB.利用平行线的性质即可解决问题;
探究:如图2中,作EG∥AB,利用平行线的性质即可解决问题;
应用:作FH∥AB,利用平行线的性质即可解决问题;
解:理由如下,
【感知】
过E点作EF//AB
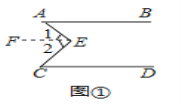
∵AB//CD
∴EF//CD
∵AB//CD
∴∠BAE=∠AEF
∵EF//CD
∴∠CEF=∠DCE
∴∠BAE+∠DCE=∠AEC.
【探究】
过E点作AB//EG.
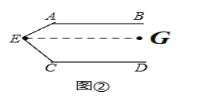
∵AB//CD
∴EG//CD
∵AB//CD
∴∠BAE+∠AEG=180°
∵EG//CD
∴∠CEG+∠DCE=180°
∴∠BAE+∠AEC+∠DCE=360°
【应用】
过点F作FH∥AB.
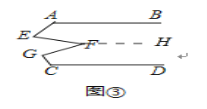
∵AB∥CD,
∴FH∥CD,
∴∠BAE+∠AEF+∠EFH=360°,∠HFG+∠FGC+∠GCD=360°,
∴∠BAE+∠AEF+∠EFH+∠HFG+∠FGC+∠GCD=720°,
∴∠BAE+∠AEF+∠EFH+∠HFG+∠FGC+∠GCD+∠EFG=720°+36°,
∴∠BAE+∠AEF+∠FGC+∠DCG=720°-360°+36°=396°
故答案为:396°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,tanB=
 ,AB=10,AC=2
,AB=10,AC=2 ,将线段AB绕点A旋转到AD,使AD∥BC,连接CD,则CD=_____.
,将线段AB绕点A旋转到AD,使AD∥BC,连接CD,则CD=_____.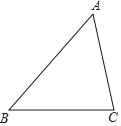
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,正方形
 中,点
中,点 ,
, 分别在边
分别在边 ,
, 上,
上, ,延长
,延长 到点
到点 ,使
,使 ,连结
,连结 ,
,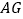 .求证:
.求证: .
.
(2)如图,等腰直角三角形
 中,
中, ,
, ,点
,点 ,
, 在边
在边 上,且
上,且 ,若
,若 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ACD中,∠B=∠D,tanB=
 ,BC=5,CD=3,∠BCA=90°﹣
,BC=5,CD=3,∠BCA=90°﹣ ∠BCD,则AD=_____.
∠BCD,则AD=_____.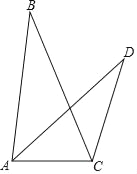
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF是Rt△ABC的中位线,∠BAC=90°,AD是斜边BC边上的中线,EF和AD相交于点O,则下列结论不正确的是( )
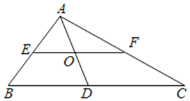
A. AO=ODB. EF=ADC. S△AEO=S△AOFD. S△ABC=2S△AEF
-
科目: 来源: 题型:
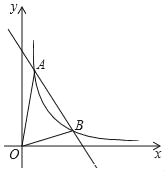
查看答案和解析>>【题目】如图一次函数y=kx+b与反比例函数y=
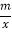 (x>0)的图象交于A(1,6),B(n,2)两点.
(x>0)的图象交于A(1,6),B(n,2)两点.(1)求一次函数和反比例函数的解析式
(2)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.

相关试题

