【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.
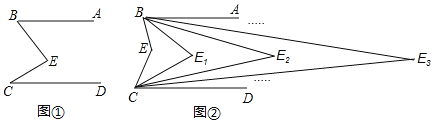
(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=![]() ∠E;
∠E;
(3)猜想:若∠En=b°,求∠BEC的度数.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)∠BEC=2nb°.
【解析】试题分析:(1)先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;
(2)先根据∠ABE和∠DCE的平分线交点为E1,运用(1)中的结论,得出∠CE1B=∠ABE1+∠DCE1= ![]() ∠ABE+
∠ABE+![]() ∠DCE=
∠DCE=![]() ∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=
∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=![]() ∠ABE1+
∠ABE1+![]() ∠DCE1=
∠DCE1=![]() ∠CE1B=
∠CE1B=![]() ∠BEC;
∠BEC;
(3)根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C=![]() ∠BEC;…据此得到规律∠En=
∠BEC;…据此得到规律∠En=![]() ∠BEC,最后求得∠BEC的度数.
∠BEC,最后求得∠BEC的度数.
试题解析:(1)如图①,过E作EF∥AB,
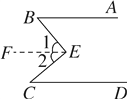
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
(2)如图2,∵∠ABE和∠DCE的平分线交点为E1,

∴由(1)可得,
∠CE1B=∠ABE1+∠DCE1=![]() ∠ABE+
∠ABE+![]() ∠DCE=
∠DCE=![]() ∠BEC;
∠BEC;
∵∠ABE1和∠DCE1的平分线交点为E2,
∴由(1)可得,
∠BE2C=∠ABE2+∠DCE2=![]() ∠ABE1+
∠ABE1+![]() ∠DCE1=
∠DCE1=![]() ∠CE1B=
∠CE1B=![]() ∠BEC;
∠BEC;
(3)如图2,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=![]() ∠ABE2+
∠ABE2+![]() ∠DCE2=
∠DCE2=![]() ∠CE2B=
∠CE2B=![]() ∠BEC;
∠BEC;
…
以此类推,∠En=![]() ∠BEC,
∠BEC,
∴当∠En=α度时,∠BEC等于2nα度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角坐标系中,A、B、D三点的坐标分别为A(8,0),B(0,4),D(﹣1,0),点C与点B关于x轴对称,连接AB、AC.
(1)求过A、B、D三点的抛物线的解析式;
(2)有一动点E从原点O出发,以每秒2个单位的速度向右运动,过点E作x轴的垂线,交抛物线于点P,交线段CA于点M,连接PA、PB,设点E运动的时间为t(0<t<4)秒,求四边形PBCA的面积S与t的函数关系式,并求出四边形PBCA的最大面积;
(3)抛物线的对称轴上是否存在一点H,使得△ABH是直角三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),….根据这个规律,第2 025个点的坐标为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡村距城市50km,甲骑自行车从乡村出发进城,出发1小时30分后,乙骑摩托车也从乡村出发进城,结果比甲先到1小时,已知乙的速度是甲的2.5倍,求甲、乙两人的速度。
【答案】甲速12km/h,乙速30km/h.
【解析】试题分析:设甲的速度是
 则乙的速度是
则乙的速度是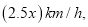 甲、乙所用时间分别为:
甲、乙所用时间分别为:  小时、
小时、 小时;根据题意可得甲比乙多用2.5小时,从而可得关于
小时;根据题意可得甲比乙多用2.5小时,从而可得关于 的方程,解方程即可解答此题;注意,最后要结合题意验根.
的方程,解方程即可解答此题;注意,最后要结合题意验根.试题解析:设甲的速度是
 则乙的速度是
则乙的速度是 根据题意列方程,得
根据题意列方程,得 整理,得
整理,得 ,
,解得:

经检验,
 是原方程的解.
是原方程的解.则

答:甲的速度是12km/h,乙的速度是30km/h.
【题型】解答题
【结束】
24【题目】已知
 求
求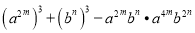 的值 。
的值 。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=1,BC=
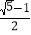 ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.

相关试题

