【题目】学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米. 
(1)求S与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)要想使矩形花圃ABCD的面积最大,AB边的长应为多少米?
参考答案:
【答案】
(1)解:由题意得:AB=x,BC=36﹣3x,S=ABBC=x(36﹣3x)=﹣3x2+36x,
即S与x之间的函数关系式为:S=﹣3x2+36x(0<x<9)
(2)解:∵S=﹣3x2+36x=﹣3(x﹣6)2+108,0<6<9
∴x=6时,S取得最大值108,
答:要想使矩形花圃ABCD的面积最大,AB边的长应为6米
【解析】(1)由题意得出AB=x,BC=36﹣3x,由矩形的面积公式即可得出S与x之间的函数关系式;(2)把函数关系式化成顶点式,由二次根式的性质即可得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.

(1)求证:CD=CB;
(2)如果⊙O的半径为 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员去年共参加
 场比赛,其中
场比赛,其中 分球的命中率为
分球的命中率为 ,平均每场有
,平均每场有 次
次 分球未投中.
分球未投中. 该运动员去年的比赛中共投中多少个
该运动员去年的比赛中共投中多少个 分球?
分球? 在其中的一场比赛中,该运动员
在其中的一场比赛中,该运动员 分球共出手
分球共出手 次,小明说,该运动员这场比赛中一定投中了
次,小明说,该运动员这场比赛中一定投中了 个
个 分球,你认为小明的说法正确吗?请说明理由.
分球,你认为小明的说法正确吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,一次函数y=kx+k与正比例函数y=kx的图像可能是( )
A.
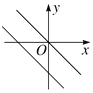 B.
B. 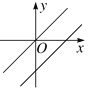 C.
C.  D.
D. 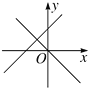
-
科目: 来源: 题型:
查看答案和解析>>【题目】为应对越来越严重的雾霾天气,孔明同学所在班级的家长委员会,准备为该班集资捐赠一台大型的空气净化机,现知道某商场将该型号的空气净化机按标价的八折出售,每台空气净化机仍可获利
 ,已知该型号客气净化机的进价为
,已知该型号客气净化机的进价为 元.
元. 求该空气净化机的标价.
求该空气净化机的标价. 若该班有
若该班有 名学生,则该班每位学生家长应平均捐助多少元.
名学生,则该班每位学生家长应平均捐助多少元. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个直七棱柱,它的底面边长都是
 ,侧棱长是
,侧棱长是 ,观察这个棱柱,请回答下列问题:
,观察这个棱柱,请回答下列问题: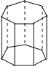
 这个七棱柱共有多少个面,它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想出
这个七棱柱共有多少个面,它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想出 棱柱有多少个面?
棱柱有多少个面? 这个七棱柱一共有多少条棱?它们的长度分别是多少?
这个七棱柱一共有多少条棱?它们的长度分别是多少? 这个七棱柱一共有多少个顶点?
这个七棱柱一共有多少个顶点? 通过对棱柱的观察,你能说出
通过对棱柱的观察,你能说出 棱柱的顶点数与
棱柱的顶点数与 的关系及棱的条数与
的关系及棱的条数与 的关系吗?
的关系吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线AB:y=5x﹣5与x轴交于点A,与y轴交于点B,点C与点B关于原点O对称,抛物线y=ax2+bx+c的对称轴为直线x=3且过点A和C.

(1)求点A和点C的坐标;
(2)求抛物线y=ax2+bx+c的解析式;
(3)若抛物线y=ax2+bx+c的顶点为D,且在x轴上存在点P使得△DAP的面积为6,直接写出满足条件的点P的坐标.
相关试题

