【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( ) 
A.不变
B.增大
C.减小
D.先变大再变小
参考答案:
【答案】C
【解析】解:∵BE⊥AD于E,CF⊥AD于F,
∴CF∥BE,
∴∠DCF=∠DBF,设CD=a,DB=b,∠DCF=∠DEB=α,
∴CF=DCcosα,BE=DBcosα,
∴BE+CF=(DB+DC)cosα=BCcosα,
∵∠ABC=90°,
∴O<α<90°,
当点D从B→D运动时,α是逐渐增大的,
∴cosα的值是逐渐减小的,
∴BE+CF=BCcosα的值是逐渐减小的.
故选C.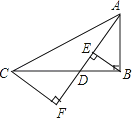
设CD=a,DB=b,∠DCF=∠DEB=α,易知BE+CF=BCcosα,根据0<α<90°,由此即可作出判断.本题考查三角函数的定义、三角函数的增减性等知识,利用三角函数的定义,得到BE+CF=BCcosα,记住三角函数的增减性是解题的关键,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.

请根据以上信息,解答下列问题:
(1)在这次调查的数据中,做作业所用时间的众数是 ,中位数是 ,平均数是 ;
(2)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)的同学共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
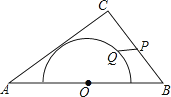
A.6
B.2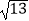 +1
+1
C.9
D.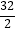
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=
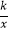 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )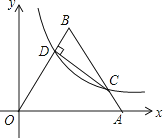
A.25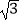
B.18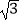
C.9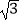
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣
 x+m与x轴、y轴分别交于A、B两点,与正比例函数y=kx交于点C(1,
x+m与x轴、y轴分别交于A、B两点,与正比例函数y=kx交于点C(1, ).
).(1)求k、m的值;
(2)求△OAC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
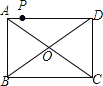
A.4.8
B.5
C.6
D.7.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
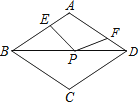
A.1
B.2
C.3
D.4
相关试题

