【题目】某中学为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.

请根据以上信息,解答下列问题:
(1)在这次调查的数据中,做作业所用时间的众数是 ,中位数是 ,平均数是 ;
(2)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)的同学共有多少人?
参考答案:
【答案】(1)3、3、3;(2)1360
【解析】试题(1)分析统计图,可以先求出平均每天完成作业所用时间为4小时的人数,补全统计图;然后根据众数,中位数的定义求出即可,用用时人数乘以完成作业时间除以50人即可求出平均完成作业的时间;(2)求出完成作业时间在3小时以内的人数除以总人数50人即可求出相应的比例,再用总人数2000人乘以这个比例即可求出每天完成作业在3小时以内的学生人数.
试题解析:(1)根据条形图可知,完成作业在4个小时的有8人,补全条形图如下:
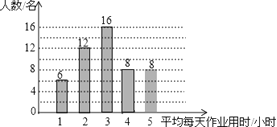
根据条形图可知完成作业时间的众数为3小时;中位数为3小时;平均数为![]()
(2)根据题意可知该校全体学生每天做作业时间在3小时内(含3小时)的同学共有![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一列按一定顺序和规律排列的数:
第一个数是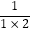 ;
;
第二个数是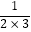 ;
;
第三个数是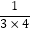 ;
;
…
对任何正整数n,第n个数与第(n+1)个数的和等于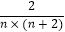 .
.
(1)经过探究,我们发现: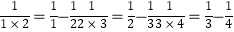
设这列数的第5个数为a,那么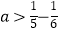 ,
, 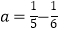 ,
, 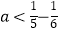 ,哪个正确?
,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于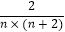 ”;
”;
(3)设M表示 ,
, 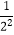 ,
, 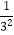 ,…,
,…, 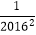 ,这2016个数的和,即
,这2016个数的和,即  ,
,
求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x
…
1
2
3
5
7
9
…
y
…
1.98
3.95
2.63
1.58
1.13
0.88
…
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整: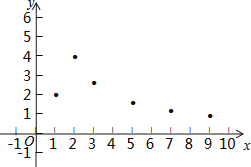
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为
②该函数的一条性质: -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )

A.
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
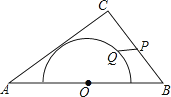
A.6
B.2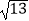 +1
+1
C.9
D.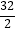
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=
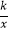 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )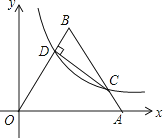
A.25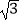
B.18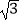
C.9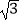
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )

A.不变
B.增大
C.减小
D.先变大再变小
相关试题

