【题目】如图,一次函数y=﹣![]() x+m与x轴、y轴分别交于A、B两点,与正比例函数y=kx交于点C(1,
x+m与x轴、y轴分别交于A、B两点,与正比例函数y=kx交于点C(1,![]() ).
).
(1)求k、m的值;
(2)求△OAC的面积.

参考答案:
【答案】(1)m=![]() ,k=
,k=![]() ;(2)2
;(2)2![]()
【解析】
(1)根据一次函数y=-![]() x+m与x轴、y轴分别交于A、B两点,与正比例函数y=kx交于点C(1,
x+m与x轴、y轴分别交于A、B两点,与正比例函数y=kx交于点C(1,![]() )可以分别求得k、m的值;
)可以分别求得k、m的值;
(2)根据题意可以求得点A的坐标,再根据点C的坐标,即可求得△OAC的面积.
(1)由题意可得,
一次函数y=﹣![]() x+m过点C(1,
x+m过点C(1,![]() ),正比例函数y=kx过点C(1,
),正比例函数y=kx过点C(1,![]() ),
),
∴![]() ,
,![]() ,
,
解得,m=![]() ,k=
,k=![]() ;
;
(2)∵一次函数y=﹣![]() x+
x+![]() 与x轴、y轴分别交于A、B两点,
与x轴、y轴分别交于A、B两点,
∴点A(4,0),点B(0,![]() ),
),
∴OA=4,OB=![]() ,
,
∵点C(1,![]() ),
),
∴△OAC的面积是:![]() =2
=2![]() .
.
-
科目: 来源: 题型:
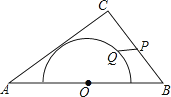
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
A.6
B.2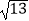 +1
+1
C.9
D.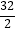
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=
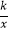 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )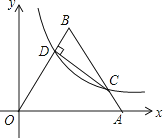
A.25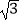
B.18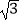
C.9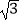
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )

A.不变
B.增大
C.减小
D.先变大再变小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
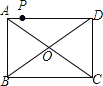
A.4.8
B.5
C.6
D.7.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
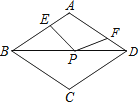
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B、C).若线段AD长为正整数,则点D的个数共有( )

A.5个
B.4个
C.3个
D.2个
相关试题

