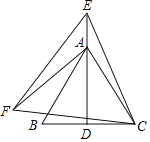
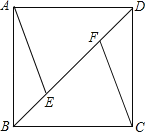
【题目】如图,D为等边△ABC中边BC的中点,在边DA的延长线上取一点E,以CE为边、在CE的左下方作等边△CEF,连结AF.若AB=4,AF=![]() ,则CF的值为_____.
,则CF的值为_____.
参考答案:
【答案】![]() .
.
【解析】
连接BF,由等边三角形的性质得出AB=AC=BC=4,CE=CF,∠ABC=∠ACB=∠BAC=∠ECF=60°,得出∠BCF=∠ACE,证明△BCF≌△ACE(SAS),得出∠CBF=∠CAE,由等边三角形的性质得出AD⊥BC,∠CAD=![]() ∠BAC=30°,由直角三角形的性质得出CD=
∠BAC=30°,由直角三角形的性质得出CD=![]() AC=2,AD=
AC=2,AD=![]() CD=2
CD=2![]() ,求出∠CAE=∠CBF=150°,得出∠ABF=90°,由勾股定理得出BF=
,求出∠CAE=∠CBF=150°,得出∠ABF=90°,由勾股定理得出BF=![]() ,得出DE=AD+AE=
,得出DE=AD+AE=![]() ,再由勾股定理即可得出答案.
,再由勾股定理即可得出答案.
解:连接BF,如图所示:
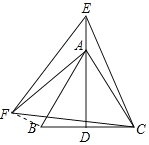
∵△ABC和△CEF是等边三角形,
∴AB=AC=BC=4,CE=CF,∠ABC=∠ACB=∠BAC=∠ECF=60°,
∴∠BCF=∠ACE,
在△BCF和△ACE中,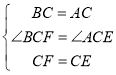 ,
,
∴△BCF≌△ACE(SAS),
∴∠CBF=∠CAE,
∵D为等边△ABC中边BC的中点,
∴AD⊥BC,∠CAD=![]() ∠BAC=30°,
∠BAC=30°,
∴CD=![]() AC=2,AD=
AC=2,AD=![]() CD=2
CD=2![]() ,∠CAE=150°,
,∠CAE=150°,
∴∠CBF=150°,
∴∠ABF=150°﹣60°=90°,
∴BF=![]() =
=![]() =
=![]() ,
,
∴AE=![]() ,
,
∴DE=AD+AE=3![]() ,
,
∴CF=CE=![]() =
=![]() =
=![]() ;
;
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A是函数y=﹣
 (x<0)图象上的一点,连结AO并延长交函数y=﹣
(x<0)图象上的一点,连结AO并延长交函数y=﹣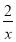 (x>0)的图象于点B,点C是x轴上一点,且AC=AO,则△ABC的面积为_____.
(x>0)的图象于点B,点C是x轴上一点,且AC=AO,则△ABC的面积为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD中,AB=4,点E,F在对角线BD上,AE∥CF.
(1)求证:△ABE≌△CDF;
(2)若∠ABE=2∠BAE,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2
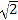 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论①△AEF≌△AED;②∠AED=45°;③BE+DC=DE; ④BE
 +DC
+DC =DE
=DE ,其中正确的是( )
,其中正确的是( )
A. ②④ B. ①④ C. ②③ D. ①③
相关试题

