【题目】点A是函数y=﹣![]() (x<0)图象上的一点,连结AO并延长交函数y=﹣
(x<0)图象上的一点,连结AO并延长交函数y=﹣![]() (x>0)的图象于点B,点C是x轴上一点,且AC=AO,则△ABC的面积为_____.
(x>0)的图象于点B,点C是x轴上一点,且AC=AO,则△ABC的面积为_____.
参考答案:
【答案】12.
【解析】
分别过A、B两点作x轴的垂线段AE、BD,则△AOE面积=![]() ×8=4,△BOD面积=
×8=4,△BOD面积=![]() ×2=1,由AO=AC,得到△AOC面积=2×△AOE面积=8.易知△OBD∽△OAE,根据面积比等于相似比的平方,于是得到结论.
×2=1,由AO=AC,得到△AOC面积=2×△AOE面积=8.易知△OBD∽△OAE,根据面积比等于相似比的平方,于是得到结论.
解:分别过A、B两点作x轴的垂线段AE、BD,
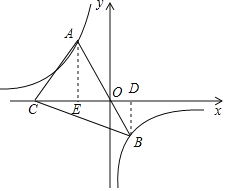
则△AOE面积=![]() ×8=4,△BOD面积=
×8=4,△BOD面积=![]() ×2=1.
×2=1.
∵AO=AC,
∴△AOC面积=2×△AOE面积=8.
∵BD∥AE,
∴△OBD∽△OAE.
∴![]() ,
,
∴![]() ,
,
∴S△BOD=![]() S△AOC=4
S△AOC=4
∴△ABC面积=8+4=12,
故答案为:12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知函数y=
 (k>0,x>0)的图象与一次函数y=mx+5(m<0)的图象相交不同的点A、B,过点A作AD⊥x轴于点D,连接AO,其中点A的横坐标为x0,△AOD的面积为2.
(k>0,x>0)的图象与一次函数y=mx+5(m<0)的图象相交不同的点A、B,过点A作AD⊥x轴于点D,连接AO,其中点A的横坐标为x0,△AOD的面积为2.(1)求k的值及x0=4时m的值;
(2)记[x]表示为不超过x的最大整数,例如:[1.4]=1,[2]=2,设t=ODDC,若﹣
 <m<﹣
<m<﹣ ,求[m2t]值.
,求[m2t]值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=5,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE.延长AF交边BC于点G,则CG为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)(6x-1)2=25;
(2)x2-2x=2x-1;
(3)x2-
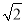 x=2;
x=2;(4)x(x-7)=8(7-x).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为等边△ABC中边BC的中点,在边DA的延长线上取一点E,以CE为边、在CE的左下方作等边△CEF,连结AF.若AB=4,AF=
 ,则CF的值为_____.
,则CF的值为_____.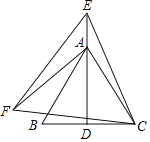
相关试题

