【题目】在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论①△AEF≌△AED;②∠AED=45°;③BE+DC=DE; ④BE![]() +DC
+DC![]() =DE
=DE![]() ,其中正确的是( )
,其中正确的是( )

A. ②④ B. ①④ C. ②③ D. ①③
参考答案:
【答案】B
【解析】
①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;
②由于∠ABC=45°,且∠AED=∠ABC+∠BAE=45°+∠BAE,而∠BAE不恒为零.可以判断是否正确;
③根据①知道△ADE≌△AFE,得CD=BF,DE=EF;由此即可确定说法是否正确;
④据①BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.
①根据旋转的性质知∠CAD=∠BAF,AD=AF,
∵∠BAC=90°,∠DAE=45°,
∴∠CAD+∠BAE=45°.
∴∠EAF=45°,
∴△AEF≌△AED;
故①正确;
②∵∠ABC=45°,且∠AED=∠ABC+∠BAE=45°+∠BAE
而∠BAE不恒为零.
故②不正确;
③根据①知道△ADE≌△AFE,得CD=BF,DE=EF,
∴BE+DC=BE+BF>DE=EF,
故③错误;
④∵∠FBE=45°+45°=90°,
∴BE2+BF2=EF2,
∵△ADC绕点A顺时针旋转90°后,得到△AFB,
∴△AFB≌△ADC,
∴BF=CD,
又∵EF=DE,
∴BE2+CD2=DE2,故④正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为等边△ABC中边BC的中点,在边DA的延长线上取一点E,以CE为边、在CE的左下方作等边△CEF,连结AF.若AB=4,AF=
 ,则CF的值为_____.
,则CF的值为_____.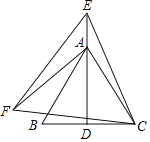
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD中,AB=4,点E,F在对角线BD上,AE∥CF.
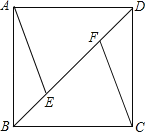
(1)求证:△ABE≌△CDF;
(2)若∠ABE=2∠BAE,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2
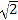 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b分别交x轴正半轴、y轴正半轴于点A、B,点P在边OA上运动(点P不与点O,A重合),PE⊥AB于点E,点F,P关于直线OE对称,PE:EA=3:4.若EF∥OA,且四边形OPEF的周长为6.

(1)求证:四边形OPEF为菱形;
(2)求证:OB=BE;
(3)求一次函数y=kx+b的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形的边长为1的方格纸中,把△ABC向右平移5个方格得△A1B1C1,再绕点B1顺时针方向旋转90°得△A2B1C2.
(1)画出平移和旋转后的图形,并标明对应字母.

(2)求顶点A从开始到结束所经过的路径的长.(结果用含有π的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角尺按如图①方式拼接:含30°角的三角尺的长直角边与含45°角的三角尺的斜边恰好重合(在Rt△ABC中,∠ACB=90°,∠BAC=30°;在Rt△ACD中,∠ADC=90°∠DAC=45°)已知AB=2
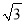 ,P是AC上的一个动点.
,P是AC上的一个动点.
(1)当PD=BC时,求∠PDA的度数;
(2)如图②,若E是CD的中点,求△DEP周长的最小值;
(3)如图③,当DP平分∠ADC时,在△ABC内存在一点Q,使得∠DQC=∠DPC,且CQ=
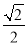 ,求PQ的长.
,求PQ的长.
相关试题

