【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?

参考答案:
【答案】(1) P,Q两点从开始出发5s时,四边形PBCQ的面积是33cm2;(2) P,Q两点从开始出发1.6s或4.8s时,点P与点Q之间的距离是10cm.
【解析】试题分析:(1)、首先设xs时面积为33,然后根据梯形的面积计算法则列出方程,从而求出答案;(2)、过点Q作QH⊥AB于H,然后求出PH的长度,最后根据Rt△PHQ的勾股定理求出未知数的值得出答案.
试题解析:解:(1)设P,Q两点从开始出发xs时,四边形PBCQ的面积是33cm2.
则由题意得![]() ×(16-3x+2x)×6=33,
×(16-3x+2x)×6=33,
解得x=5.(3分)∵16÷3=![]() >5,
>5,
∴x=5符合题意.
故P,Q两点从开始出发5s时,四边形PBCQ的面积是33cm2;
(2)设P,Q两点从开始出发ys时,点P与Q之间的距离是10cm,
过点Q作QH⊥AB于H,
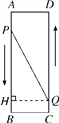
∴∠QHA=90°.∵四边形ABCD是矩形,∴∠A=∠D=90°,
∴四边形ADQH是矩形,∴AH=DQ=(16-2y)cm,QH=AD=6cm,
∴当P点在H点上方时,PH=AH-AP=16-2y-3y=(16-5y)(cm);当P点在H点下方时,PH=AP-AH=3y-(16-2y)=(5y-16)(cm), ∴PH=|16-5y|cm.
在Rt△PQH中,根据勾股定理得PH2+QH2=PQ2,
即(16-5y)2+62=102,解得y1=1.6,y2=4.8. ∵16÷3=![]() ,
,
∴y1=1.6和y2=4.8均符合题意.
故P,Q两点从开始出发1.6s或4.8s时,点P与点Q之间的距离是10cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列四项调查中,方式正确的是


A. 了解本市中学生每天学习所用的时间,采用全面调查的方式
B. 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式
C. 了解某市每天的流动人口数,采用全面调查的方式
D. 了解全市中学生的视力情况,采用抽样调查的方式
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2
(1)求实数k的取值范围。
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值。
-
科目: 来源: 题型:
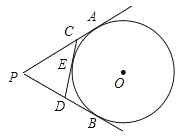
查看答案和解析>>【题目】如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是( )
A.
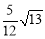 B.
B.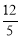 C.
C. D.
D.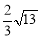
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一条直线过点
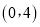 ,且与抛物线
,且与抛物线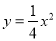 交于A、B两点,其中点A的横坐标是-2.
交于A、B两点,其中点A的横坐标是-2.⑴求这条直线的函数关系式及点B的坐标 ;
⑵在
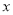 轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在点C,使得ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由; ⑶.过线段AB上一点P,作PM∥
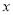 轴,交抛物线于点M,点M在第一象限;点
轴,交抛物线于点M,点M在第一象限;点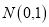 ,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
,当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是______.

相关试题

