【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
. 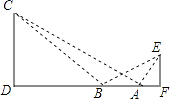
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
参考答案:
【答案】
(1)解:∵∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() ,
,
∴tan60°= ![]() ,tan30°=
,tan30°= ![]() ,
,
解得,EF=5 ![]() ,AF=5,
,AF=5,
即旗杆EF的高为5 ![]() 米
米
(2)解:∵∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() ,AF=5,
,AF=5,
∴CD=BD, ![]() ,
,
设CD=3a,则BD=3a,AD=4a,
∴AB=a=10,
∴BD=3a=30,
∴DF=AD+AF=40+5=45,
即旗杆EF与实验楼CD之间的水平距离DF的长是45米
【解析】(1)根据题目中的数据和锐角三角函数可以求得EF和AF的长,从而可以解答本题;(2)根据题目中的数据和锐角三角函数可以求得AD和AF的长,从而可以得到旗杆EF与实验楼CD之间的水平距离DF的长.
-
科目: 来源: 题型:
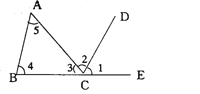
查看答案和解析>>【题目】如图:∠1和∠4是AB、_______被_______所截得的________角,∠3和∠5是_______、_____被_______所截得的_________角,∠2和∠5是______、_______被_______所截得的________角,AC、BC被AB所截得的同旁内角是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.
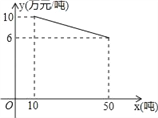
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=x+4的图象与反比例函数y=
 (k为常数,且k≠0)的图象交于A(﹣1,a),B(b,1)两点.
(k为常数,且k≠0)的图象交于A(﹣1,a),B(b,1)两点.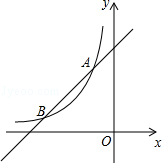
(1)求反比例函数的表达式;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
(3)求△PAB的面积. -
科目: 来源: 题型:
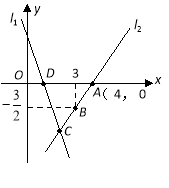
查看答案和解析>>【题目】如图,直线
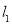 的解析表达式为
的解析表达式为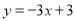 ,且
,且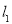 与
与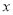 轴交于点
轴交于点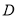 ,直线
,直线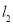 经过点
经过点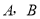 ,直线
,直线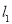 ,
, 交于点
交于点 .
.
(1)求点
 的坐标;
的坐标;(2)求直线
 的解析表达式;
的解析表达式;(3)求
 的面积。
的面积。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、DC被BD所截得的内错角是___________,AB、CD被AC所截是的内错角是_________,AD、BC被BD所截得的内错角是_________,AD、BC被AC所截得的内错角是_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=
 AC,连接CE、OE,连接AE交OD于点F.
AC,连接CE、OE,连接AE交OD于点F. 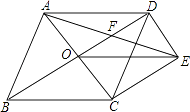
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
相关试题

