【题目】如图,正方形![]() 的边长为1,点
的边长为1,点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的负半轴上将正方形
轴的负半轴上将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至正方形
至正方形![]() 的位置,
的位置,![]() 与
与![]() 相交于点
相交于点![]() ,则
,则![]() 的坐标为____________.
的坐标为____________.

参考答案:
【答案】![]()
【解析】连接AM,由旋转性质知AD=AB′=1、∠BAB′=30°、∠B′AD=60°,证Rt△ADM≌Rt△AB′M得∠DAM=![]() ∠B′AD=30°,由DM=ADtan∠DAM可得答案.
∠B′AD=30°,由DM=ADtan∠DAM可得答案.
如图,连接AM,
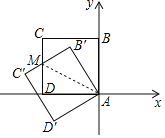
∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C′D′,
∴AD=AB′=1,∠BAB′=30°,
∴∠B′AD=60°,
在Rt△ADM和Rt△AB′M中,
∵![]() ,
,
∴Rt△ADM≌Rt△AB′M(HL),
∴∠DAM=∠B′AM=![]() ∠B′AD=30°,
∠B′AD=30°,
∴DM=ADtan∠DAM=1×![]() =
=![]() ,
,
∴点M的坐标为(-1,![]() ),
),
故答案为:(-1,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:①已知A(x1,y1)、B(x2,y2),则AB=
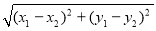 ;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离
;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离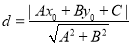
(1)已知 A2,5、 B1,1,求 AB ;
(2)已知 A2,1,直线l : 3x 4y 5 0,求 A 到直线的距离;
(3)求两平行直线3x 4y1 0与3x 4 y 8 0之间的距离;
(4)求
 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
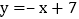 与正比例函数
与正比例函数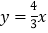 的图象交于点
的图象交于点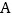 ,且与
,且与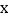 轴交于点
轴交于点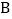 .
.(1)直接写出点
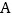 的坐标为 ;点
的坐标为 ;点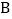 的坐标为 ;
的坐标为 ;(2)过点
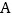 作
作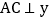 轴于点
轴于点 ,过点
,过点 作直线l∥y轴.动点
作直线l∥y轴.动点 从点
从点 出发,以每秒
出发,以每秒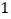 个单位长的速度,沿
个单位长的速度,沿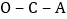 的路线向点
的路线向点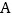 运动;同时直线
运动;同时直线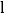 从点
从点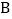 出发,以相同速度向左平移,在平移过程中,直线
出发,以相同速度向左平移,在平移过程中,直线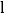 交
交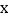 轴于点
轴于点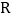 ,交线段
,交线段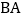 或线段
或线段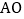 于点
于点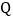 .当点
.当点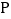 到达点
到达点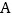 时,点
时,点 和直线
和直线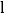 都停止运动.在运动过程中,设动点
都停止运动.在运动过程中,设动点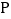 运动的时间为
运动的时间为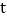 秒.
秒. 当
当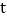 为何值时,以
为何值时,以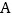 、
、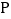 、
、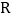 为顶点的三角形的面积为
为顶点的三角形的面积为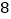 ;
; 是否存在以
是否存在以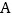 、
、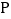 、
、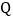 为顶点的三角形是等腰三角形?若存在,直接写出
为顶点的三角形是等腰三角形?若存在,直接写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.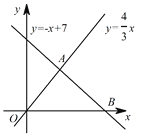
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
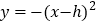 (
(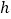 为常数),当自变量
为常数),当自变量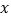 的值满足
的值满足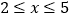 时,与其对应的函数值
时,与其对应的函数值 的最大值为-1,则
的最大值为-1,则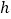 的值为( )
的值为( )A. 3或6 B. 1或6 C. 1或3 D. 4或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年10月18日至27日(共10天)武汉军运会期间,从19日起武汉体育中心9天中接收观众人数的变化情况如下表(正数表示比前一天多的人数,负数表示经前一天少的人数):
日期
19日
20日
21日
2日
23日
24日
25日
26日
27日
人数变化/万人
+0.5
+0.7
+0.8
-0.4
-0.6
+0.2
+0.3
+0.5
+0.2
(1)请判断这9天中,游客人数最多和最少的各是哪一天?它们相差多少万人?
(2)如果10月18日观众人数为2万人,平均每人门票100元,请问武汉体育中心在军运会这10天期间门票总收入为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区要在一块长方形的空地上修建三条人行道(阴影部分),其余空地铺设草坪进行美化,设计规划如图所示,长方形空地长为m米,宽为n米,且三条人行道宽均为2米.
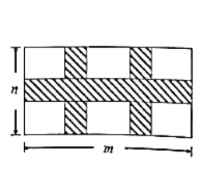
(1)请直接写出草坪面积是多少平方米?(用m,n表示)
(2)若n=18,且人行道所占面积为整个长方形空地面积的
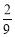 ,则该长方形空地的长为多少米?
,则该长方形空地的长为多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,
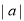 的几何意义是数轴上表示数a的点与原点的距离,一般地,点A,B在数轴上分别表示数a,b,那么A,B之间的距离可表示为|a-b|,请根据绝对值的几何意义并结合数轴解答下列问题:
的几何意义是数轴上表示数a的点与原点的距离,一般地,点A,B在数轴上分别表示数a,b,那么A,B之间的距离可表示为|a-b|,请根据绝对值的几何意义并结合数轴解答下列问题:(1)数轴上的数x与1所对应的点的距离为________,数x与-1所对应的点的距离为________;
(2)求
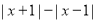 的最大值;
的最大值;(3)直接写出
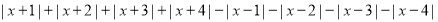 的最大值为______.
的最大值为______.
相关试题

