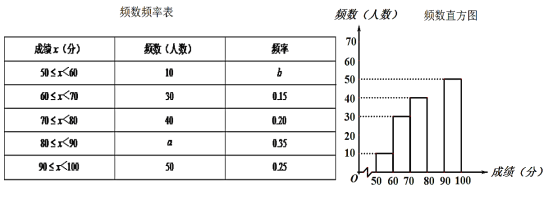
【题目】为传承中华优秀传统文化,某校团委组织了一次全校![]() 名学生参加的“汉字书写”大赛,为了解本次大赛的成绩,校团委随机抽取了其中
名学生参加的“汉字书写”大赛,为了解本次大赛的成绩,校团委随机抽取了其中![]() 名学生的成绩(成绩
名学生的成绩(成绩![]() 取整数,总分
取整数,总分![]() 分)作为样本进行统计,制成如下不完整的统计图表:
分)作为样本进行统计,制成如下不完整的统计图表:
根据所给信息,解答下列问题:
(1)![]() _____,
_____,![]() ______;
______;
(2)补全频数直方图;
(3)这![]() 名学生成绩的中位数会落在______分数段;
名学生成绩的中位数会落在______分数段;
(4)若成绩在![]() 分以上(包括
分以上(包括![]() 分)为“优”等,请你估计该校参加本次比赛的
分)为“优”等,请你估计该校参加本次比赛的![]() 名学生中成绩为“优”等的有多少人。
名学生中成绩为“优”等的有多少人。
参考答案:
【答案】(1)70,0.05;(2)见解析;(3)80≤x<90;(4)625人.
【解析】
(1)根据第一组的频数是30,频率是0.15,求得数据总数,再用数据总数乘以第四组频率可得a的值,用第一组频数除以数据总数可得b的值;
(2)根据(1)的计算结果即可补全频数分布直方图;
(3)根据中位数的定义,将这组数据按照从小到大的顺序排列后,处于中间位置的数据(或中间两数据的平均数)即为中位数;
(4)利用总数2500乘以“优”等学生的所占的频率即可.
(1)本次调查的总人数为30÷0.15=200,
则a=200×0.35=70,b=10÷200=0.05,
故答案为:70,0.05;
(2)频数分布直方图如图所示,
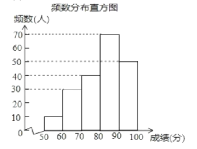
(3)200名学生成绩的中位数是第100、101个成绩的平均数,而第100、101个数均落在80x<90,
∴这200名学生成绩的中位数会落在80x<90分数段,
故答案为:80x<90;
(4)该校参加本次比赛的3000名学生中成绩“优”等的约有:2500×0.25=625(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-2x+2的图象与
 轴、
轴、 轴分别交于点
轴分别交于点 、
、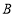 ,以线段
,以线段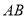 为直角边在第一象限内作等腰直角三角形ABC,且
为直角边在第一象限内作等腰直角三角形ABC,且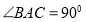 ,则点C坐标为_____.
,则点C坐标为_____.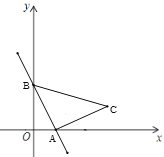
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(1)①∠BCE与∠CDF的大小关系是_______________;
②证明:GF⊥BF;
(2)探究G落在边DC的什么位置时,BF=BC,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和OA+OB+OC+OD最小,正确的作法是连接AC、BD交于点O,则点O就是要找的点,请你用所学过的数学知识解释这一道理__________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】铜仁市积极推动某公园建设,通过旅游带动一方经济,计划经过若干年使公园绿化总面积新增450万平方米.自2016年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可以提前3年完成任务.
(1)求实际每年绿化面积是多少万平方米
(2)为加大公园绿化力度,市政府决定从2019年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点A(6
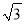 ,0),点B(0,18),∠BAO=60°,射线AC平分∠BAO交y轴正半轴于点C.
,0),点B(0,18),∠BAO=60°,射线AC平分∠BAO交y轴正半轴于点C.(1)求点C的坐标;
(2)点N从点A以每秒2个单位的速度沿线段AC向终点C运动,过点N作x轴的垂线,分别交线段AB于点M,交线段AO于点P,设线段MP的长度为d,点P的运动时间为t,请求出d与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,将△ABO沿y轴翻折,点A落在x轴正半轴上的点E,线段BE交射线AC于点D,点Q为线段OB上的动点,当△AMN与△OQD全等时,求出t值并直接写出此时点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)
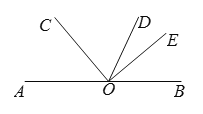
解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
相关试题

