【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的是( )

A. AE=BE B. DE⊥CE C. CD=AD+BC D. CD=AD+CE
参考答案:
【答案】D
【解析】
根据直角梯形、等腰三角形的判定与性质以及全等三角形的判定与性质进行分析、 判断,可得正确的选择.
解:B,![]() AD//BC,
AD//BC,![]() ∠ADC+∠BCD=180,
∠ADC+∠BCD=180,
![]() ED平分∠ADC,EC平分∠BCD,
ED平分∠ADC,EC平分∠BCD,
![]() ∠EDC=
∠EDC=![]() ∠ADC, ∠DCE=
∠ADC, ∠DCE=![]() ∠DCB,
∠DCB,
![]() ∠EDC+∠DCE=
∠EDC+∠DCE=![]()
![]() 180
180![]() =90
=90![]() ,
,
![]() ∠DEC=180
∠DEC=180![]() -90
-90![]() =90
=90![]() ,
,
故B选项不符合题意;
A、C选项,延长DE交CB的延长线于点F. 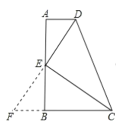
![]() AD//BC, DE是∠ADC的角平分线,
AD//BC, DE是∠ADC的角平分线,
![]() ∠CDF=∠ADE=∠DFC ,
∠CDF=∠ADE=∠DFC ,
![]() CD=CF,
CD=CF,
![]() △CDF 是等腰三角形;
△CDF 是等腰三角形;
又由前面得DE⊥EC,
![]() DE=FE,
DE=FE,
又![]() ∠AED=∠BEF,
∠AED=∠BEF,
![]() △BEF≌△AED,
△BEF≌△AED,
![]() AE=EB,
AE=EB,
故A选项不符合题意;
![]() AD=BF,又
AD=BF,又![]() CD=CF,
CD=CF,
![]() CD=CF=BC+BF=AD+BC,
CD=CF=BC+BF=AD+BC,
故C选项不符合题意,
无法得出D选项,
故本题答案:D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则
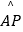 与
与  的长度之和为( )
的长度之和为( ) 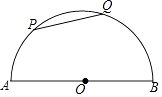
A.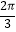
B.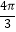
C.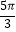
D.π -
科目: 来源: 题型:
查看答案和解析>>【题目】木工师傅要做一个如图所示的窗框,上半部分是半圆,下半部分为六个大小一样的长方形,长方形的长和宽的比为
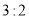 .请你帮他计算:
.请你帮他计算: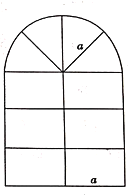
(1)设长方形的长为
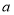 米,用含
米,用含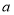 的代数式表示所需材料的长度为 (结果保留
的代数式表示所需材料的长度为 (结果保留 ,重合部分忽略不计)
,重合部分忽略不计)(2)当长方形的长为
 米时,所需材料的长度是多少?(精确到
米时,所需材料的长度是多少?(精确到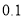 米,其中
米,其中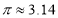 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知数轴上有三点A、B、C,它们对应的数分别为a、b、c,且c-b=b-a;点C对应的数是10.
(1)若BC=15,求a、b的值;
(2)如图2,在(1)的条件下,O为原点,动点P、Q分别从A、C同时出发,点P向左运动,运动速度为2个单位长度/秒,点Q向右运动,运动速度为1个单位长度/秒,N为OP的中点,M为BQ的中点.
①用含t代数式表示PQ、 MN;
②在P、Q的运动过程中,PQ与MN存在一个确定的等量关系,请指出他们之间的关系,并说明理由.
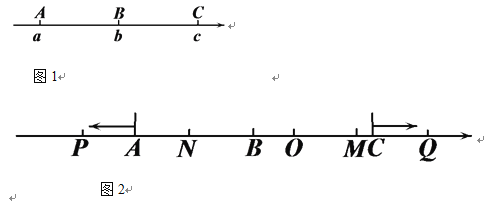
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:
(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);
(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);
(3)将纸片收展平,那么∠AFE的度数为( )

A. 60° B. 67.5° C. 72° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】现规定:求若千个相同的有理数(均不等于
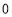 )的商的运算叫做除方,比如
)的商的运算叫做除方,比如 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把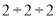 记作
记作 ,读作“
,读作“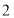 的圈
的圈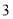 次方”,
次方”, 记作
记作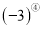 ,读作“
,读作“ 的圈
的圈 次方”,一般地,把
次方”,一般地,把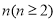 个
个
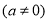 相除记作
相除记作 ,读作“
,读作“ 的圈
的圈 次方”.
次方”.初步探究:(1)直接写出结果:
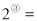 .
. .
.(2)下列关于除方的说法中,错误的是
A.任何非零数的圈
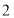 次方都等于
次方都等于
B.对于任何正整数
 的圈
的圈 次方等于
次方等于
C.
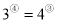
D.负数的圈奇数次方的结果是负数,负数的圈偶数次方的结果是正数
深入思考:我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(3)试一试,把下列除方运算直接写成幂的形式
 .
. .
.(4)想一想,请把有理数
 的圈
的圈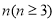 次方写成幂的形式.
次方写成幂的形式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.

(1)这个几何体模型的名称是
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足 a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
相关试题

