【题目】现规定:求若千个相同的有理数(均不等于![]() )的商的运算叫做除方,比如
)的商的运算叫做除方,比如![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”,
次方”,![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”,一般地,把
次方”,一般地,把![]() 个
个![]()
![]() 相除记作
相除记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”.
次方”.
初步探究:(1)直接写出结果:![]() .
.![]() .
.
(2)下列关于除方的说法中,错误的是
A.任何非零数的圈![]() 次方都等于
次方都等于![]()
B.对于任何正整数![]() 的圈
的圈![]() 次方等于
次方等于![]()
C.![]()
D.负数的圈奇数次方的结果是负数,负数的圈偶数次方的结果是正数
深入思考:我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(3)试一试,把下列除方运算直接写成幂的形式![]() .
. .
.
(4)想一想,请把有理数![]() 的圈
的圈![]() 次方写成幂的形式.
次方写成幂的形式.
参考答案:
【答案】(1) ![]() ;(2)C;(3)
;(2)C;(3)![]() ;(4)
;(4)![]()
【解析】
(1)分别按公式进行计算即可;
(2)根据定义依次判定即可;
(3)把除法化为乘法,根据幂的乘方进行计算;
(4)把除法化为乘法,第一个数和第二个数不变,做除法,得1,从第三个数开始依次变为乘法,乘以它的倒数,结果为(n-2)个![]() 相乘,由此改成幂的形式即可.
相乘,由此改成幂的形式即可.
解:(1)有题意可知:![]() ,
,
![]()
故答案为:![]() ;
;
(2)A、任何非零数的圈2次方都等于1;所以选项A正确;
B、因为多少个1相除都是1,所以对于任何正整数n,1都等于1;所以选项B正确;
C、3④=3÷3÷3÷3=![]() ,4③=4÷4÷4=
,4③=4÷4÷4=![]() ,则3④≠4③;所以选项C错误;
,则3④≠4③;所以选项C错误;
D、负数的圈奇数次方,相当于奇数个负数相除,则结果是负数,负数的圈偶数次方,相当于偶数个负数相除,则结果是正数.所以选项D正确;
本题选择说法错误的,
故选C;
(3)![]()
![]()
故答案为:![]() ;
;
(4)a的圈n次方=
∴把有理数![]() 的圈
的圈![]() 次方写成幂的形式为
次方写成幂的形式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知数轴上有三点A、B、C,它们对应的数分别为a、b、c,且c-b=b-a;点C对应的数是10.
(1)若BC=15,求a、b的值;
(2)如图2,在(1)的条件下,O为原点,动点P、Q分别从A、C同时出发,点P向左运动,运动速度为2个单位长度/秒,点Q向右运动,运动速度为1个单位长度/秒,N为OP的中点,M为BQ的中点.
①用含t代数式表示PQ、 MN;
②在P、Q的运动过程中,PQ与MN存在一个确定的等量关系,请指出他们之间的关系,并说明理由.
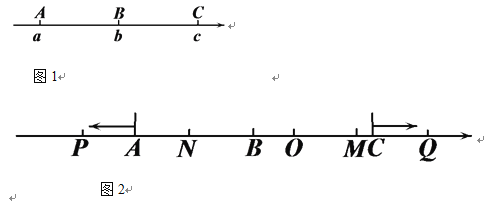
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的是( )

A. AE=BE B. DE⊥CE C. CD=AD+BC D. CD=AD+CE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:
(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);
(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);
(3)将纸片收展平,那么∠AFE的度数为( )

A. 60° B. 67.5° C. 72° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.

(1)这个几何体模型的名称是
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足 a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积. -
科目: 来源: 题型:
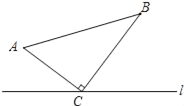
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=5cm,BC=12cm.动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥MN于E,QF⊥MN于F.则点P运动时间为_____秒时,△PEC与△QFC全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

相关试题

