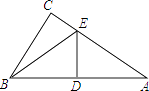
【题目】已知：如图，△ABC中的顶点A、C分别在平面直角坐标系的x轴、y轴上，且∠ACB=90°，AC=2，BC=1，当点A从原点出发朝x轴的正方向运动，点C也随之在y轴上运动，当点C运动到原点时点A停止运动，连结OB．

（1）点A在原点时，求OB的长；
（2）当OA=OC时，求OB的长；
（3）在整个运动过程中，OB是否存在最大值？若存在，请你求出这个最大值；若不存在，请说明理由．

参考答案：

【答案】
（1）

解：点A在原点时，OB=AB，

∵∠ACB=90°，AC=2，BC=1，

∴AB= = = ；

∴OB=


（2）

解：当OA=OC时，如图1，作BD⊥y轴于D，

∵AC=2，BC=1，

∵OA2+OC2=AC2，

∴OA=OC= ，

∵OA=OC，

∴∠ACO=45°，

∵∠ACB=90°，

∴∠BCD=45°，

∴∠BCD=∠CBD，

∴DB=DC，

∵DC2+DB2=BC2，

∴DB=DC= ，

∴OD=OC+DC= + = ，

∴OB= = =


（3）

解：如图2，作AC的中点D，连接OD、BD，

∵OB≤OD+BD，

∴当O、D、B三点共线时OB取得最大值，

∵BD= = = ，OD=AD= AC=1，

∴点B到原点O的最大距离为1+ ．


【解析】（1）根据题意AB的长就是OB的长，根据勾股定理求得AB的长即可；（2）作BD⊥y轴于D，根据勾股定理可得OC= ，DC=DB= ，最后根据勾股定理即可求得OB；（3）Rt△AOC的外接圆圆心是AC中点，设AC中点为D，根据三角形三边关系有OB≤OD+BD=1+ ，即O、D、B三点共线时OB取得最大值．
【考点精析】本题主要考查了两点间的距离的相关知识点，需要掌握同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记才能正确解答此题．

关闭