【题目】如图,△ABC中,∠C=90°,边AB的垂直平分线交AB、AC边分别为点D,点E,连结BE. 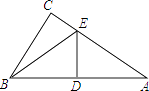
(1)若∠A=40°,求∠CBE的度数.
(2)若AB=10,BC=6,求△BCE的周长.
参考答案:
【答案】
(1)解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠A=∠ABE=40°,
∵Rt△ABC中,∠C=90°,∠A=40°,
∴∠ABC=50°,
∴∠CBE=∠ABC﹣∠ABE=10°
(2)解:∵∠C=90°,AB=10,BC=6,
∴AC=8,
∵DE是AB的垂直平分线,
∴AE=BE,
∴BE+CE=AC=8,
∴△BCE的周长=BE+CE+BC=AC+BC=14
【解析】(1)由AB的垂直平分线DE交AC于点E,可得AE=BE,继而求得∠ABE的度数,然后由Rt△ABC中,∠C=90°,求得∠ABC的度数,继而求得答案;(2)根据勾股定理得到AC=8,根据线段的垂直平分线的性质得到AE=BE,即可得到结论.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中的顶点A、C分别在平面直角坐标系的x轴、y轴上,且∠ACB=90°,AC=2,BC=1,当点A从原点出发朝x轴的正方向运动,点C也随之在y轴上运动,当点C运动到原点时点A停止运动,连结OB.

(1)点A在原点时,求OB的长;
(2)当OA=OC时,求OB的长;
(3)在整个运动过程中,OB是否存在最大值?若存在,请你求出这个最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列是用火柴棒拼出的一列图形.

仔细观察,找出规律,解答下列各题:
(1)第5个图中共有根火柴;
(2)第n个图形中共有根火柴(用含n的式子表示);
(3)请计算第2013个图形中共有多少根火柴? -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=-(x-1)2-2的顶点坐标是( )
A. (-1,2)B. (-1,-2)C. (1,-2)D. (1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,属于真命题的是( )
A.同位角相等
B.正比例函数是一次函数
C.平分弦的直径垂直于弦
D.对角线相等的四边形是矩形 -
科目: 来源: 题型:
查看答案和解析>>【题目】经过平面上的三点中的任两点可以画直线( )
A. 3条 B. 1条 C. 1条或3条 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是 ( )
A.(a-2b) (a-2b)=a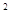 -4b
-4b 
B.(P-q)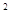 =P
=P 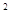 -q
-q 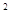
C.(a+2b) (a-2b)=-a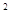 -2b
-2b 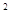
D.(-s-t)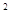 =s
=s 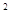 +2st+t
+2st+t 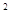
相关试题

