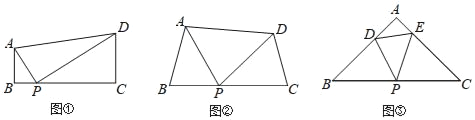
【题目】如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90° 时,可知△ABP∽△PCD.(不要求证明)
(1)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
(2)拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上若∠B=∠C=∠DPE=45°,BC=8![]() ,CE=6,则DE的长为 .
,CE=6,则DE的长为 .
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】【试题分析】(1)根据两角对应相等,两三角形相似证明;(2)根据相似三角形的性质求解.
【试题解析】
∵∠APD=90°,
∴∠APB+∠DPC=90°,
∵∠B=90°,
∴∠APB+∠BAP=90°,
∴∠BAP=∠DPC,
∵AB∥CD,∠B=90°,
∴∠C=∠B=90°,
∴△ABP∽△DCP.
(1)探究:∵∠APC=∠BAP+∠B,∠APC=∠APD+∠CPD,
∴∠BAP+∠B=∠APD+∠CPD.
∵∠B=∠APD,
∴∠BAP=∠CPD.
∵∠B=∠C,
∴△ABP∽△PCD,
(2)拓展:同探究的方法得出,△BDP∽△CPE,
∴![]() ,
,
∵点P是边BC的中点,
∴BP=CP=4![]() ,
,
∵CE=6,
∴![]() ,
,
∴BD=![]() ,
,
∵∠B=∠C=45°,
∴∠A=180°﹣∠B﹣∠C=90°,
即AC⊥AB且AC=AB=8,
∴AD=AB﹣BD=8﹣![]() =
=![]() ,AE=AC﹣CE=2,
,AE=AC﹣CE=2,
在Rt△ADE中,DE=![]() =
=![]() .
.
故答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
 ,AD平分∠CAB,交CB于点D,过点D作
,AD平分∠CAB,交CB于点D,过点D作 于点E.若
于点E.若 ,CD=5,.
,CD=5,.(1)求BD的长
(2)AE与BE相等吗?说明理由。
(3)求△ABC的面积

-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好
 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.10月1日
2日
3日
4日
5日
6日
7日
4
3
2
0
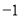


 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天? 直接回答,不必写过程
直接回答,不必写过程 .
. 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则
 周长的最小值为______.
周长的最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,△ABC是等腰锐角三角形,AB=AC(
 ),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;(2)如图2,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线;
(3)如图3,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数(如有需要,可在答题卡相应位置另外画图).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
(1)线段AE的长为 .(用含t的代数式表示)
(2)若△ADE与△ACB的面积比为1:4时,求t的值.
(3)设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.
(4)当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
相关试题

