搜索
【题目】如图，在△ABC中,
，AD平分∠CAB，交CB于点D，过点D作
于点E．若
，CD=5，．
（1）求BD的长
（2）AE与BE相等吗？说明理由。
（3）求△ABC的面积
参考答案：
【答案】（1）BD=10；（2）
，理由见解析；(3) △ABC的面积为
.
【解析】试题分析：（1）根据角平分线性质求出
的长根据含
角的直角三角形性质求出
即可．
（2）AE与BE相等，证明
是等腰三角形，利用等腰三角形的性质即可证明
根据
求出
的长度，根据三角形的面积公式求解即可.
试题解析：(1)∵AD平分∠CAB,
，DE⊥AB，
∴CD=DE=5，
∵
∴BD=2DE=10，
(2)AE与BE相等，理由如下：
∵在△ABC中,
∴
∵AD平分∠CAB交CB于点D，
∴
∴AD=BD，
∵DE⊥AB，
∴AE=BE.
在
中，
设
则
即
解得：
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，
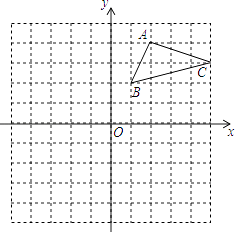
（1）画出△ABC关于x轴对称的△A1B1C1 ．
（2）画出△ABC绕原点O旋转180°后的△A2B2C2 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△OAB中，∠OAB=90°，OA=AB=6，将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 ．
（1）线段A1B1的长是 ， ∠AOA1的度数是；
（2）连结AA1 ， 求证：四边形OAA1B1是平行四边形；
（3）求四边形OAA1B1的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．
（1）求抛物线的解析式；
（2）若点D为该抛物线上的一个动点，且在直线AC上方，当以A，C，D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】在有些情况下，不需要计算出结果也能把绝对值符号去掉．例如：
|6＋7|＝6＋7；|6－7|＝7－6；|7－6|＝7－6；|－6－7|＝6＋7；
根据上面的规律，把下列各式写成去掉绝对值符号的形式：
(1)|7－21|＝_________；
(2)|
|＝____________；(3)|
|＝__________；(4)用合理的方法计算：|
|＋|
|－
×|－|＋
. -
科目： 来源： 题型：
查看答案和解析>>【题目】观察、猜想、探究：
在△ABC中，
．（1）如图①，当
，AD为∠BAC的角平分线时，求证：
；（2）如图②，当
，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明；
（3）如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？不需要证明，请直接写出你的猜想.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将两条宽度都为3的纸条重叠在一起，使∠ABC=60°，则四边形ABCD的面积为 ．
相关试题
