【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

参考答案:
【答案】10
【解析】
连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.
解:连接AD,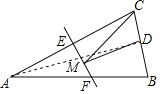
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=![]() BCAD=
BCAD=![]() ×4×AD=16,解得AD=8,
×4×AD=16,解得AD=8,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+![]() BC=8+
BC=8+![]() ×4=8+2=10.
×4=8+2=10.
故答案为:10.
-
科目: 来源: 题型:
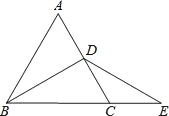
查看答案和解析>>【题目】如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店用1000元购进一批套尺,很快销售一空;商店又用1500元购进第二批同款套尺,购进单价比第一批贵25%,所购数量比第一批多100套.
(1)求第一批套尺购进的单价;
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有
 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为 元(利润=收入-支出).
元(利润=收入-支出).(1)请写出
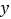 与
与 的关系式 ;
的关系式 ;(2)完成表格.
 人
人500
1000
1500
2000
2500
3000
…
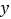 元
元…
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
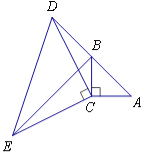
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE= cm;
(3)BE与AD有何位置关系?请说明理由.
相关试题

