【题目】在小学,我们知道正方形具有性质“四条边都相等,四个内角都是直角”,请适当利用上述知识,解答下列问题:
已知:如图,在正方形ABCD中,AB=4,点G是射线AB上的一个动点,以DG为边向右作正方形DGEF,作EH⊥AB于点H.
(1)填空:∠AGD+∠EGH= °;
(2)若点G在点B的右边.
①求证:△DAG≌△GHE;
②试探索:EH﹣BG的值是否为定值,若是,请求出定值;若不是,请说明理由.
(3)连接EB,在G点的整个运动(点G与点A重合除外)过程中,求∠EBH的度数;

参考答案:
【答案】(1)90;(2)①答案见解析;②EH﹣BG的值是定值4;(3)45°.
【解析】试题分析:(1)根据正方形的性质得到∠DGE=90°,由平角的定义即可得到结论;
(2)①根据垂直的定义得到∠GHE=90°,根据余角的性质得到∠GEH=∠AGD,根据正方形的性质得到∠DAG=90°,DG=GE,求得∠DAG=∠GHE,根据全等三角形的判定定理即可得到结论;②根据全等三角形的性质得到AG=EH,根据线段的和差即可得到结论;
(3)下面分两种情况讨论:( I)当点G在点B的左侧时,如图1,根据全等三角形的性质得到GH=DA=AB,EH=AG,于是得到GB+BH=AG+GB,推出△BHE是等腰直角三角形,根据等腰直角三角形的性质得到∠EBH=45°;( II)如图2,当点G在点B的右侧时,根据全等三角形的想知道的GH=DA=AB,EH=AG,于是得到AB+BG=BG+GH,推出△BHE是等腰直角三角形,根据等腰直角三角形的性质得到∠EBH=45°;( III)当点G与点B重合时,如图3,根据全等三角形的性质得到GH=DA=AB,EH=AG=AB,推出△GHE(即△BHE)是等腰直角三角形,于是得到∠EBH=45°即可得到结论.
试题解析:解: (1)90;
(2)①∵EH⊥AB,
∴∠GHE![]() 90°,
90°,
∴∠GEH+∠EGH![]() 90°,
90°,
又∠AGD+∠EGH![]() 90°,
90°,
∴∠GEH![]() ∠AGD,
∠AGD,
∵四边形ABCD与四边形DGEF都是正方形,
∴∠DAG![]() 90°,DG
90°,DG![]() GE,
GE,
∴∠DAG![]() ∠GHE,
∠GHE,
在△DAG和△GHE中,
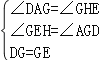 ,
,
∴△DAG≌△GHE(AAS);
②EH﹣BG的值是定值,
理由如下:由①证得:△DAG≌△GHE,
∴AG![]() EH,
EH,
又AG![]() AB
AB![]() BG,AB
BG,AB![]() 4,
4,
∴EH![]() AB+BG,EH﹣BG
AB+BG,EH﹣BG![]() AB
AB![]() 4;
4;
(3)下面分两种情况讨论:
(I)当点G在点B的左侧时,如图1,
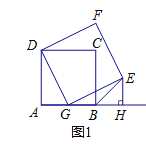
同(2)①可证得:△DAG≌△GHE,
∴GH![]() DA
DA![]() AB,EH
AB,EH![]() AG,
AG,
∴GB+BH![]() AG+GB,
AG+GB,
∴BH![]() AG
AG![]() EH,又∠GHE
EH,又∠GHE![]() 90°
90°
∴△BHE是等腰直角三角形,
∴∠EBH![]() 45°;
45°;
( II) 如图2,当点G在点B的右侧时,
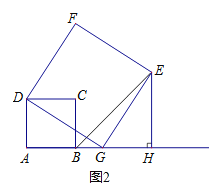
由(2)①证得:△DAG≌△GHE.
∴GH![]() DA
DA![]() AB,EH
AB,EH![]() AG,
AG,
∴AB+BG![]() BG+GH,
BG+GH,
∴AG![]() BH,又EH
BH,又EH![]() AG
AG
∴EH![]() HB,又∠GHE
HB,又∠GHE![]() 90°
90°
∴△BHE是等腰直角三角形,
∴∠EBH![]() 45°;
45°;
( III)当点G与点B重合时,
如图3,同理可证:△DAG≌△GHE,
∴GH![]() DA
DA![]() AB,EH
AB,EH![]() AG
AG![]() AB,
AB,
∴△GHE(即△BHE)是等腰直角三角形,
∴∠EBH![]() 45°
45°
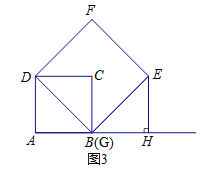
综上,在G点的整个运动(点G与点A重合除外)过程中,∠EBH都等于45°。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|3x-6|+(y+3)2=0,则3x+2y的值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两列火车同时从相距700千米的两地相向而行,甲列车每小时行85千米.乙列车每小时行90千米,几小时两列火车相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.



-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别从相距30千米的A、B两地同时相向而行,经过3小时后相距3千米,再经过2小时,甲到B地所剩的路程是乙到A地所剩路程的2倍,试求甲、乙两人的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P的坐标为(0,﹣5),以P为圆心的圆与x轴相切,⊙P的弦AB(B点在A点右侧)垂直于y轴,且AB=8,反比例函数
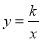 (k≠0)经过点B,则k=______.
(k≠0)经过点B,则k=______. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着奥运会成功召开,福娃系列商品也随之热销.一天小林在商场看到一件奥运吉祥物的纪念品,标价为每件33元,他的身边只带有2元和5元两种面值的人民币各若干张,他买了一件这种商品. 若无需找零钱,则小林付款方式有哪几种(指付出2元和5元钱的张数)?哪种付款方式付出的张数最少?
相关试题

