【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于点B和A,与反比例函数的图像交于C、D,CE⊥x轴于点E,若![]() ,OB=4,OE=2,点D的坐标为(6,m).
,OB=4,OE=2,点D的坐标为(6,m).
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积。

参考答案:
【答案】(1)直线AB的解析式是:y=12x+2,反比例函数的解析式是:y=![]() ;
;
(2)S△COD= 8.
【解析】试题分析:(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例的函数解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解.
试题解析:(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E, tan∠ABO=![]() =
=![]() .
.
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为(4,0)、点C的坐标为(2,3).
设直线AB的解析式为y=kx+b,
则![]() ,
,
解得: 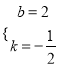 .
.
故直线AB的解析式为y=![]() x+2.
x+2.
设反比例函数的解析式为y=![]() .
.
将点C的坐标代入,得3=![]() ,
,
∴m=6.
∴该反比例函数的解析式为y= ![]() .
.
(2)联立反比例函数的解析式和直线AB的解析式可得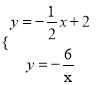 ,
,
可得交点D的坐标为(6,1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8.
-
科目: 来源: 题型:
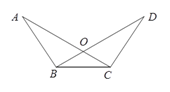
查看答案和解析>>【题目】如图,AC、BD相交于点O,AB=CD,AC=BD.求证:(1) ∠ABD=∠DCA;(2) AO=DO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每逢金秋送爽之时,正是大闸蟹上市的旺季,也是吃蟹的最好时机,可谓膏肥黄美.九月份,某经销商购进一批雌蟹、雄蟹共1000只,进价均为每只40元,然后以雌蟹每只75元、雄蟹每只60元的价格售完,共获利29000元.
(1)求该经销商分别购进雌蟹、雄蟹各多少只?
(2)民间有“九雌十雄”的说法,即九月吃雌蟹,十月吃雄蟹.十月份,在进价不变的情况下该经销商决定调整价格,将雌蟹的价格在九月份的基础上下调
 (降价后售价不低于进价),雄蟹的价格上涨
(降价后售价不低于进价),雄蟹的价格上涨 ,同时雌蟹的销量较九月下降了
,同时雌蟹的销量较九月下降了 ,雄蟹的销量上升了
,雄蟹的销量上升了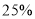 ,结果十月份的销售额比九月份增加了1000元,求a的值.
,结果十月份的销售额比九月份增加了1000元,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】汽车油箱内存油45L,每行驶100km耗油10L,行驶过程中油箱内剩余油量yL与行驶路程skm的函数关系式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若“”是某种新规定的运算符号,设ab=3a+2b,则[(x+y)(x﹣y)]3x化简为( )
A.0
B.21x+3y
C.5x
D.9x+6y -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点A(m,3)与点B(4,n)关于y轴对称,那么(m+n)2016的值为( )
A. ﹣1 B. 1 C. ﹣72016 D. 72016
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形两边的长分别为3和8,那么这个三角形的周长是 .
相关试题

