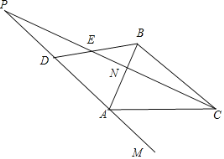
【题目】如图,已知△ABC,∠A=∠B=70°.请按如下要求操作并解答:

(1)在图中,过点A画直线MP∥BC,过点C画直线NP⊥AB,直线MP与NP交于点P,求∠APC的度数;
(2)在(1)的前提下,直线PM上存在点D,且∠ABD=∠ADB,求直线BD与直线PN相交所形成的锐角的度数.
参考答案:
【答案】(1)∠APC=20°;(2)直线BD与直线PN相交所形成的锐角的度数为35°.
【解析】
(1) 先作图,再根据内错角定理即可求出∠APC的度数.
(2) 根据MP∥BC可得∠ADB+∠CBD,再求得∠ABD=∠ADB=55,∠BEN=90°-∠BNE即可解答
解:(1)如图所示,∵PC⊥AB,
∴∠CNB=90°,
∵∠ABC=70°,
∴∠BCN=20°,
∵MP∥BC,
∴∠APC=∠BCN=20°;
(2)∵MP∥BC,
∴∠ADB+∠CBD=180°,
∵∠ABD=∠ADB,∠ABC=70°,
∴∠ABD=∠ADB=55°,
∵∠BNE=90°,
∴∠BEN=90°﹣55°=35°,
∴直线BD与直线PN相交所形成的锐角的度数为35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形
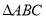 中,
中,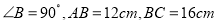 ,点
,点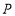 从
从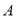 开始沿
开始沿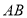 边向点
边向点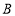 以
以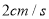 的速度移动,点
的速度移动,点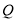 从点
从点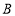 开始沿
开始沿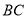 边向点
边向点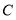 以
以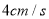 的速度移动.
的速度移动. 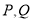 分别从
分别从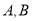 同时出发,当一个动点到达终点则另一动点也随之停止运动,
同时出发,当一个动点到达终点则另一动点也随之停止运动,(1)求
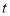 为何值时,
为何值时,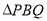 为等腰三角形?
为等腰三角形?(2)是否存在某一时刻
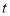 ,使点
,使点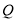 在线段
在线段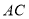 的垂直平分线上?
的垂直平分线上?(3)点
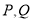 在运动的过程中,是否存在某时刻
在运动的过程中,是否存在某时刻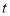 , 直线
, 直线 把
把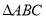 的周长分为
的周长分为 两部分?若存在,求出
两部分?若存在,求出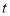 ,若不存在,请说明理由.
,若不存在,请说明理由.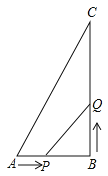
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两站的路程是312km,一列列车从甲站开往乙站,设列车的平均速度为xkm/h,所需时间为yh.
(1)试写出y关于x的函数关系式;
(2)2006年全国铁路第六次大提速前,这列列车从甲站到乙站需要4h,列车提速后,速度提高了26km/h,问提速后从甲站到乙站需要几个小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在新罗区中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要5.5万元,购买2台电脑和1台电子白板需要5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过50万元,则最多能购买电子白板多少台?
-
科目: 来源: 题型:
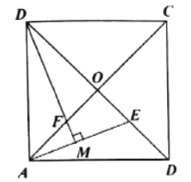
查看答案和解析>>【题目】如图,正方形
 的对角线
的对角线 ,
, 相交于点
相交于点 .
.
(1) (2)
(1)若点
 是
是 上一点,连接
上一点,连接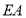 ,过点
,过点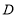 作
作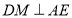 ,垂足为
,垂足为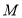 ,
,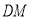 与
与 相交于点
相交于点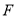 .求证:
.求证: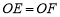 ;
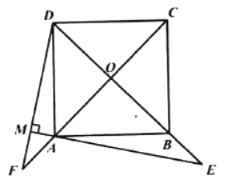
;(2)若点
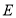 在
在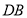 的延长线上,
的延长线上,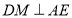 于点
于点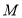 ,
,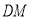 交
交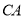 的延长线于点
的延长线于点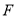 ,其他条件不变结论“
,其他条件不变结论“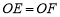 ”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
”还成立吗?如果成立,请给出证明;如果不成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一般的,数a的绝对值|a|表示数a对应的点与原点的距离.同理,绝对值|a﹣b|表示数轴上数a对应的点与数b对应的点的距离.例如:|3﹣0|指在数轴上表示数3的点与原点的距离,所以3的绝对值是3,即|3﹣0|=|3|=3.|6﹣2|指数轴上表示6的点和表示2的点的距离,所以数轴上表示6的点和表示2的点的距离是4,即|6﹣2|=4.
结合数轴与绝对值的知识解答下列问题:
(1)解含绝对值的方程|x+2|=1得x的解为 ;
(2)解含绝对值的不等式|x+5|<3得x的取值范围是 ;
(3)求含绝对值的方程
 的整数解;
的整数解;(4)解含绝对值的不等式|x﹣1|+|x﹣2|>4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD⊥AC,AE⊥BC,AE、BD交于点O,连接CO,∠ABC=54°,∠ACB=48°,则∠COD=( )

A. 51°B. 66°C. 78°D. 88°
相关试题

