【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图1,在矩形纸片ABCD和矩形纸片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,点E是AD的中点,矩形纸片EFGH以点E为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图1,当EF与AB相交于点M,EH与BC相交于点N时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当AM=CN时,AM与BM有怎样的数量关系,说明理由.
(3)“创新”小组提出的问题是;若矩形EFGH继续以点E为旋转中心进行逆时针旋转,当∠AEF=60°时,请你在图2中画出旋转后的示意图,并求出此时EF将边BC分成的两条线段的长度.
参考答案:
【答案】
(1)
解:如图1,过点E作EP⊥BC,垂足为点P,
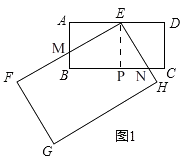
则四边形ABPE是矩形,
∴PE=AB=1,∠AEP=90°,
∵点E是AD的中点,
∴AE=DE= ![]() AD=1,
AD=1,
∴PE=AE,
∵∠MEN=∠AEP=90°,
∴∠MEN﹣∠MEP=∠AEP﹣∠MEP,
∴∠PEN=∠AEM,
∵PE=AE,∠EPN=∠EAM=90°,
∴△PEN≌△AEM,
∴EM=EN
(2)
解:由(1)知,△PEN≌△AEM,
∴AM=PN,
∵AM=CN,
∴PN=CN= ![]() PC,
PC,
∵四边形EPCD是矩形,
∴PC=DE=1,PN=CN= ![]() ,
,
∴AM=PN= ![]() ,BM=AB﹣AM=
,BM=AB﹣AM= ![]() ,
,
∴AM=BM
(3)
解:如图2,
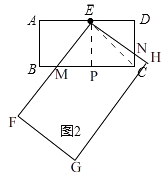
当∠AEF=60°时,
设EF与BC交于M,EH与CD交于N,过点E作EP⊥BC于P,连接EC,
由(1)知,CP=EP=1,AD∥BC,
∴∠EMP=∠AEF=60°,
在Rt△PEM中,PM= ![]() =
= ![]() ,
,
∴BM=BP﹣PM=1﹣ ![]() ,CM=PC+PM=1+
,CM=PC+PM=1+ ![]() ,
,
∴EF将边BC分成的两条线段的长度为1﹣ ![]() ,1+
,1+ ![]() .
.
【解析】(1)先判断出PE=AE,再判断出∠PEN=∠AEM,进而得到△PEN≌△AEM,即可得出结论;(2)先判断出PN=CN= ![]() PC,进而求出PN=CN=
PC,进而求出PN=CN= ![]() ,再判断出AM=PN,即可得出BM=
,再判断出AM=PN,即可得出BM= ![]() ,结论得证;(3)在直角三角形PEM中,求出PM,再用线段的和差即可得出结论.
,结论得证;(3)在直角三角形PEM中,求出PM,再用线段的和差即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A是抛物线y=
 x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当m=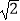 时,求S的值.
时,求S的值.
(2)求S关于m(m≠2)的函数解析式.
(3)①若S= 时,求
时,求  的值;
的值;
②当m>2时,设 =k,猜想k与m的数量关系并证明.
=k,猜想k与m的数量关系并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED灯泡
普通白炽灯泡
进价(元)
45
25
标价(元)
60
30

(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=
 AB中,一定正确的是( )
AB中,一定正确的是( ) 
A.①②③
B.①②④
C.①③④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3 , 则下列结论不一定成立的是( )
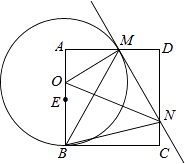
A.S1>S2+S3
B.△AOM∽△DMN
C.∠MBN=45°
D.MN=AM+CN -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.

(1)求抛物线的函数表达式,并求出点D的坐标;
(2)如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(3)在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在⊙O的直径AB上,AB=6,AC=1.点P为⊙O上的任意一点,当∠OPC取最大值时,则△OCP的面积为 .
相关试题

