【题目】学校准备在各班设立图书角以丰富同学们的课余文化生活,为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:


(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
(5)学校若在喜爱艺术、文学、科普、体育四类中任意抽取两类建立兴趣小组,求出恰好选中是体育和科普两类的概率?
参考答案:
【答案】(1)300人. (2)补图见解析;(3)![]() ; (4)480人;(5)
; (4)480人;(5)![]() .
.
【解析】试题分析:
(1)由折线图知喜爱文学的人数,由扇形统计图可知喜爱文学学生所占的百分比,则此则可求出参加调查学生的总数;
(2)结合折线图与扇形图计算出喜爱艺术的人数和其他的人数;
(3)用喜爱体育学生点总人数的百分比乘以360°;
(4)用样本估计总体,通过300个中喜爱科普类书籍估计结果;
(5)这是一个等可能事件,画出树状图,列出所有可能的结果,是科普和体育的结果,从而计算出是体育和科普两类的概率.
试题解析:
(1)调查的学生人数为:90÷30%=300人.
(2)如图
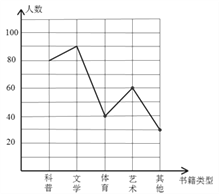
(3)喜爱体育书籍的学生人数为: 300―80―90―60―30=40.
体育部分所对的圆心角为: ![]() .
.
(4)在抽样调查中,喜欢科普类书籍所占比例为: ![]() ,可以估计,在全校同学中,喜欢科普类书籍的人数大约占了
,可以估计,在全校同学中,喜欢科普类书籍的人数大约占了![]() , 人数约为1800×
, 人数约为1800×![]() =480人.
=480人.
(5)画出树状图:
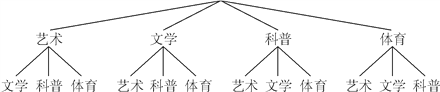
∴P(选中恰是体育和科普)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段
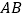 ,
, 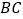 ,
, 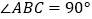 . 求作:矩形
. 求作:矩形 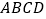 .
.
以下是甲、乙两同学的作业:
甲:① 以点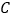 为圆心,
为圆心, 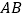 长为半径作弧;
长为半径作弧;
② 以点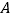 为圆心,
为圆心, 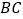 长为半径作弧;
长为半径作弧;
③ 两弧在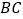 上方交于点
上方交于点 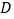 ,连接
,连接 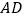 ,
, 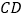 .
.
四边形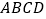 即为所求矩形.(如图)
即为所求矩形.(如图)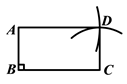
乙:① 连接 ,作线段
,作线段  的垂直平分线,交
的垂直平分线,交  于点
于点 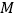 ;
;
② 连接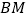 并延长,在延长线上取一点
并延长,在延长线上取一点 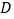 ,使
,使 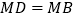 ,连接
,连接 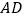 ,
, 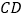 .
.
四边形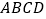 即为所求矩形.(如图)
即为所求矩形.(如图)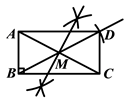
老师说甲、乙同学的作图都正确.
则甲的作图依据是:;
乙的作图依据是:. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果a与1互为相反数,则|a+2|等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】试确定 22014·32015的个位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程:
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化成为x+3=2
解得x=-1,经检验x=-1是方程的解;
当x+3<0,原方程可化为,-(x+3)=2
解得x=-5,经检验x=-5是方程的解.
所以原方程的解是x=-1,x=-5.
解答下面的两个问题:
(1)解方程:|3x-2|-4=0;
(2)探究:当值a为何值时,方程|x-2|=a , ①无解;②只有一个解;③有两个解. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知C为线段AB的中点,D为线段AC的中点.
(1)画出相应的图形,求出图中线段的条数并写出相应的线段;
(2)若图中所有线段的长度和为26,求线段AC的长度. -
科目: 来源: 题型:
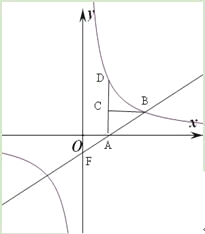
查看答案和解析>>【题目】如图,点D在双曲线上,AD垂直
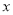 轴,垂足为
轴,垂足为A,点C在AD上,CB平行于
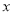 轴交双曲线于点B,直线AB与
轴交双曲线于点B,直线AB与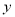 轴交于点F,已知AC:
轴交于点F,已知AC:AD=1:3,点C的坐标为(2,2)。
(1)求该双曲线的解析式;
(2)求△OFA的面积。
相关试题

