【题目】已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E,CE=AC.
(1)求证:四边形ABCD是矩形;
(2)若AB=4,AD=3,求四边形BCED的周长.
参考答案:
【答案】(1)详见解析;(2)16.
【解析】
(1)根据已知条件推知四边形BCED是平行四边形,则对边相等:CE=BD,依据等量代换得到对角线AC=BD,则平行四边形ABCD是矩形;
(2)通过勾股定理求得BD的长度,再利用四边形BCED是平行四边形列式计算即可得解.
(1)证明:∵四边形ABCD是平行四边形,
∴AE∥BC.
∵CE∥BD,
∴四边形BCED是平行四边形.
∴CE=BD.
∵CE=AC,
∴AC=BD.
∴□ABCD是矩形.
(2)解:∵□ABCD是矩形,AB=4,AD=3,
∴∠DAB=90°,BC=AD=3,
∴![]() .
.
∵四边形BCED是平行四边形,
∴四边形BCED的周长为2(BC+BD)=2×(3+5)=16.
故答案为(1)详见解析;(2)16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题14分)如图(1),在△ABC和△EDC中,D为△ABC边AC上一点,CA平分∠BCE,BC=CD,AC=CE.


(1)求证:△ABC≌△EDC;
(2)如图(2),若∠ACB=60°,连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.
①求∠DHF的度数;
②若EB平分∠DEC,试说明:BE平分∠ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】瑞士的一位中学教师巴尔末从光谱数据
 ,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
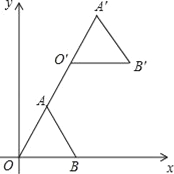
A. (4,2
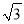 ) B. (3,3
) B. (3,3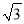 ) C. (4,3
) C. (4,3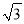 ) D. (3,2
) D. (3,2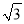 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某农民收了400多个橙子(不到500个),把这些橙子20个装一盒或者12个装一盒,都是多5个,这个农民一共收了______个橙子.
-
科目: 来源: 题型:
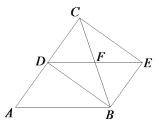
查看答案和解析>>【题目】如图,已知ABED,延长AD到C使AD=DC,连接BC,CE,BC交DE于点F,若AB=BC.
(1)求证:四边形BECD是矩形;
(2)连接AE,若∠BAC=60°,AB=4,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程.
(1)x2﹣x﹣1=0;
(2)x2﹣2x=2x+1;
(3)x(x﹣2)﹣3x2=﹣1;
(4)(x+3)2=(1﹣2x)2.
相关试题

