【题目】(本题14分)如图(1),在△ABC和△EDC中,D为△ABC边AC上一点,CA平分∠BCE,BC=CD,AC=CE.


(1)求证:△ABC≌△EDC;
(2)如图(2),若∠ACB=60°,连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.
①求∠DHF的度数;
②若EB平分∠DEC,试说明:BE平分∠ABC.
参考答案:
【答案】(1)略 (2)①∠DHF=60° ② 略
【解析】(1)∵CA平分∠BCE,
∴∠ACB=∠ACE.
在△ABC和△EDC中
∵BC=CD,∠ACB=∠ACE,AC=CE
∴△ABC≌△EDC(SAS)
(2)①在△BCF和△DCG中
∵BC=DC, ∠BCD=∠DCE,CF=CG,
∴△BCF≌△DCG(SAS),
∴∠CBF=∠CDG.
∵∠CBF+∠BCF=∠CDG+∠DHF
∴∠BCF=∠DHF=60°.
②∵EB平分∠DEC,
∴∠DEH=∠BEC.
∵∠DHF=60°,
∴∠HDE=60°-∠DEH.
∵∠BCE=60°+60°=120°,
∴∠CBE=180°-120°-∠BEC=60°-∠BEC.
∴∠HDE=∠CBE. ∠A=∠DEG.
∵△ABC≌△EDC, △BCF≌△DCG(已证)
∴∠∠BFC=∠DGC,
∵∠ABF=∠BFC-∠A, ∠HDE=∠DGC-∠DEG,
∴∠ABF=∠HDE,
∴∠ABF=∠CBE,
∴BE平分∠ABC.
-
科目: 来源: 题型:
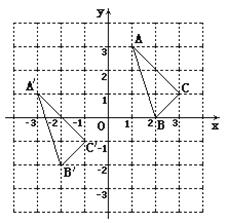
查看答案和解析>>【题目】△ A B C与
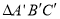 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.(1)分别写出下列各点的坐标:
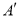 ______ ;
______ ; 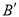 _______ ;
_______ ; 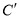 _______ ;
_______ ;(2)说明
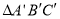 由△ A B C经过怎样的平移得到? ________________________________.
由△ A B C经过怎样的平移得到? ________________________________.(3)若点
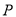 (
( ,
, 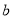 )是△ A B C内部一点,则平移后
)是△ A B C内部一点,则平移后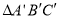 内的对应点
内的对应点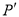 的坐标为 ________ ;
的坐标为 ________ ;(4)求△ A B C的面积..
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学毕业生响应国家“自主创业”的号召,投资开办了一个装饰品商店.该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=﹣2x+80(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=
 (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).(1)试写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)分别与销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
注:销售利润=销售收入﹣购进成本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点D在边BC上,DE⊥AB于E,DH⊥AC于H,且满足DE=DH,F为AE的中点,G为直线AC上一动点,满足DG=DF,若AE=4cm,则AG= _____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.

(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( ).
A. (-4,-1) B. (-1,-4) C. (5,-4) D. (-5,-4)
相关试题

