【题目】用适当的方法解下列方程.
(1)x2﹣x﹣1=0;
(2)x2﹣2x=2x+1;
(3)x(x﹣2)﹣3x2=﹣1;
(4)(x+3)2=(1﹣2x)2.
参考答案:
【答案】(1)x1=![]() ,x2=
,x2=![]() (2)x1=2+
(2)x1=2+![]() ,x2=2﹣
,x2=2﹣![]() (3)x1=
(3)x1=![]() ,x2=
,x2=![]() (4)x1=﹣
(4)x1=﹣![]() ,x2=4
,x2=4
【解析】试题分析:(1)、利用公式法来进行求解,即![]() ,将a、b、c代入进行计算即可得出答案;(2)、利用配方法进行求解,得出方程的解;(3)、首先将方程整理成一般式,然后利用公式法求出方程的解;(4)、首先根据平方差公式将方程进行因式分解,然后求出方程的解.
,将a、b、c代入进行计算即可得出答案;(2)、利用配方法进行求解,得出方程的解;(3)、首先将方程整理成一般式,然后利用公式法求出方程的解;(4)、首先根据平方差公式将方程进行因式分解,然后求出方程的解.
试题解析:(1)x2﹣x﹣1=0; 这里a=1,b=﹣1,c=﹣1,
△=b2﹣4ac=(﹣1)2﹣4×1×(﹣1)=5. x=![]() =
=![]() ,
,
所以:x1=![]() ,x2=
,x2=![]() .
.
(2)移项,得x2﹣4x=1, 配方,得x2﹣4x+4=1+4, 即(x﹣2)2=5.
两边开平方,得x﹣2=±![]() , 即x=2±
, 即x=2±![]() , 所以x1=2+
, 所以x1=2+![]() ,x2=2﹣
,x2=2﹣![]() .
.
(3)x(x﹣2)﹣3x2=﹣1, 整理,得2x2+2x﹣1=0, 这里a=2,b=2,c=﹣1,
△=b2﹣4ac=22﹣4×2×(﹣1)=12.
x=![]() =
=![]() =
=![]() ,
,
即原方程的根为x1=![]() ,x2=
,x2=![]() .
.
(4)移项,得(x+3)2﹣(1﹣2x)
因式分解,得(x+3+1﹣2x)[x+3﹣(1﹣2x)]=0,
整理,得(3x+2)(﹣x+4)=0, 解得x1=﹣![]() ,x2=4.
,x2=4.
-
科目: 来源: 题型:
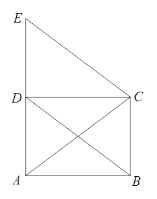
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E,CE=AC.
(1)求证:四边形ABCD是矩形;
(2)若AB=4,AD=3,求四边形BCED的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农民收了400多个橙子(不到500个),把这些橙子20个装一盒或者12个装一盒,都是多5个,这个农民一共收了______个橙子.
-
科目: 来源: 题型:
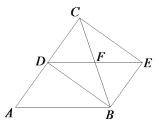
查看答案和解析>>【题目】如图,已知ABED,延长AD到C使AD=DC,连接BC,CE,BC交DE于点F,若AB=BC.
(1)求证:四边形BECD是矩形;
(2)连接AE,若∠BAC=60°,AB=4,求AE的长.
-
科目: 来源: 题型:
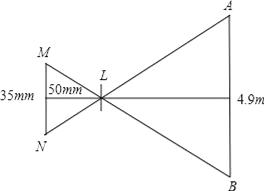
查看答案和解析>>【题目】如图,是一个照相机成像的示意图,像高MN,景物高度AB、
CD为水平视线,根据物体成像原理知:AB∥MN,CD⊥MN.
(1)如果像高MN是35mm,焦距CL是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物的距离LD是多少?
(2)如果要完整的拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少毫米?
-
科目: 来源: 题型:
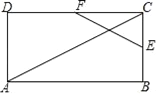
查看答案和解析>>【题目】如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动,如果E、F同时出发,用t(0≤t≤6)秒表示运动的时间,当t为何值时,以点E、C、F为顶点的三角形与△ACD相似?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B 种纪念品可获利润30元,在(2)的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
相关试题

