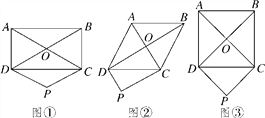
【题目】如图①,矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP.
(1)判断四边形CODP的形状并说明理由;
(2)如图②,如果题目中的矩形变为菱形,判断四边形CODP的形状并说明理由;
(3)如图③,如果题目中的矩形变为正方形,判断四边形CODP的形状并说明理由.
参考答案:
【答案】(1)四边形CODP是菱形,理由见解析; (2)四边形CODP是矩形,理由见解析;(3)四边形CODP是正方形,理由见解析.
【解析】试题分析:(1)根据矩形的性质得出OD=OC,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据菱形的判定推出即可;
(2)根据菱形的性质得出∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据矩形的判定推出即可;
(3)根据正方形的性质得出OD=OC,∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据正方形的判定推出即可;
试题解析:
(1)四边形CODP的形状是菱形,理由是:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴OC=OD,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵OC=OD,
∴平行四边形CODP是菱形;
(2)四边形CODP的形状是矩形,
理由是:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵∠DOC=90°,
∴平行四边形CODP是矩形;
(3)四边形CODP的形状是正方形,
理由是:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴∠DOC=90°,OD=OC,
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形,
∵∠DOC=90°,OD=OC
∴平行四边形CODP是正方形.
-
科目: 来源: 题型:
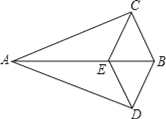
查看答案和解析>>【题目】如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.
求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
-
科目: 来源: 题型:
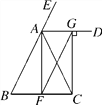
查看答案和解析>>【题目】如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG;
(2)当AC⊥FG时,△ABC应是怎样的三角形?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图所示,在四边形ABCD中,AB=2
 ,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点 B(m,n) 在第一象限,m,n 均为整数,且满足n =
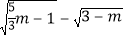 .
.(1) 求点 B 的坐标;
(2) 将线段 OB 向下平移 a 个单位后得到线段 O′B′,过点 B′作 B′C⊥y 轴于点 C,若 3CO=2CO′,求a 的值;
(3) 过点 B 作与 y 轴平行的直线 BM,点 D 在 x 轴上,点 E 在 BM 上,点 D 从 O 点出发以每秒钟 3个单位长度的速度沿 x 轴向右运动,同时点 E 从 B 点出发以每秒钟 2 个单位长度的速度沿BM 向下运动,在点 D,E 运动的过程中,若直线 OE,BD 相交于点 G,且 5≤S△OGB≤10,则点G 的横坐标 xG的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

相关试题

