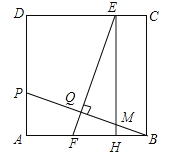
【题目】如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.
参考答案:
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)由EQ⊥BO,EH⊥AB得到∠EQN=∠BHM=90°,由∠EMQ=∠BMH得到△EMQ∽△BMH,故∠QEM=∠HBM.由ASA定理得到△APB≌△HFE,故可得出结论;
(2)根据勾股定理求出BP的长,由EF是BP的垂直平分线可知BQ=![]() BP,再由锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=
BP,再由锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=![]() ,再由EQ=EF﹣QF即可得出结论.
,再由EQ=EF﹣QF即可得出结论.
试题解析:(1)∵EQ⊥BO,EH⊥AB,∴∠EQN=∠BHM=90°,∵∠EMQ=∠BMH,∴△EMQ∽△BMH,∴∠QEM=∠HBM,在Rt△APB与Rt△HFE中,∵∠QEM=∠HBM,∠PAB=∠FHE,AB=EH,∴△APB≌△HFE,∴HF=AP;
(2)由勾股定理得,BP=![]() =
=![]() =4
=4![]() ,∵EF是BP的垂直平分线,∴BQ=
,∵EF是BP的垂直平分线,∴BQ=![]() BP=
BP=![]() ,∴QF=BQtan∠FBQ=BQtan∠ABP=
,∴QF=BQtan∠FBQ=BQtan∠ABP=![]() =
=![]() ,由(1)知,△APB≌△HFE,∴EF=BP=
,由(1)知,△APB≌△HFE,∴EF=BP=![]() ,∴EQ=EF﹣QF=
,∴EQ=EF﹣QF=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在有理数中,绝对值等于它本身的数有( )
A.1个
B.2个
C.3个
D.无穷多个 -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题:解下列各式
(1)解方程组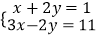
(2)解不等式组: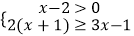 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连结BE、CF.
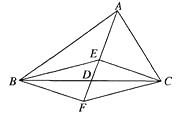
(1)图中的四边形BFCE是平行四边形吗?为什么?
(2)若AB=AC,其它条件不变,那么四边形BFCE是菱形吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=90°,AB=AC点D为直线BC上一动点(点D不与B、C重合) .以AD为边作正方形ADEF,连接CF.

(1)如图①,当点D在线段BC上时,求证:①BD⊥CF;②CF=BCCD.
(2)如图②,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF、BC、CD三条线段之间的关系.
(3)如图③,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其他条件不变:①请直接写出CF、BC、CD三条线段之间的关系;②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为6 cm、3 cm,则该等腰三角形的周长是( )
A.9 cm B.12 cm C.12 cm或 15 cm D.15 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a是一元二次方程x2﹣3x﹣5=0的一个根,那么代数式8﹣a2+3a的值为:
A.1B.2C.3D.4
相关试题

