【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.

参考答案:
【答案】(1)∠PFD+∠AEM=90°(2)证明见解析(3)45°
【解析】分析:(1)由AB∥CD可得∠PFD与∠AEM的等于∠P;(2)∠1+∠PFD=180°,由对顶角相等,分别将∠1,∠AEM转化为∠PHE与∠2;(3)由∠PEB=15°得∠PHE和∠1,又AB∥CD,则∠1=∠PFC,而∠PFC=∠N+∠DON.
详解:(1)过P作平行线,由AB∥CD易得∠PFD与∠AEM的等于∠P,所以∠PFD与∠AEM的数量关系为 ∠PFD+∠AEM=90° ;
(2)证明:如图②所示:
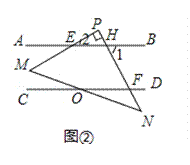
∵AB∥CD,∴∠PFD+∠1=180°,
∵∠P=90°,∴∠PHE+∠2=90°,
∵∠2=∠AEM,∴∠1=∠PHE=90°﹣∠AEM,
∴∠PFD+90°﹣∠AEM=180°,
∴∠PFD﹣∠AEM=90°;
(3)如图②所示:
∵∠P=90°,∴∠PHE=90°﹣∠PEB=90°﹣15°=75°,
∵AB∥CD,∴∠PFC=∠PHE=75°,
∵∠PFC=∠N+∠DON,
∴∠N=75°﹣30°=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),求点B的坐标.
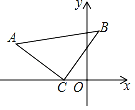
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣
 x2﹣3x﹣
x2﹣3x﹣  ,设自变量的值分别为x1 , x2 , x3 , 且﹣3<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系是( )
,设自变量的值分别为x1 , x2 , x3 , 且﹣3<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系是( )
A.y1>y2>y3
B.y1<y2<y3
C.y2>y3>y1
D.y2<y3<y1 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)(x3)2.(﹣x4)3 (2)(
 x5y4﹣
x5y4﹣ x4y3)
x4y3) x3y3
x3y3(3)2mn.[(2mn)2﹣3n(mn+m2n)] (4)(2a+1)2﹣(2a+1)(2a﹣1)
(5)102+
 ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302| -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣x+a(a>0),当自变量x取m时,其相应的函数值y<0,那么下列结论中正确的是( )
A.m﹣1的函数值小于0
B.m﹣1的函数值大于0
C.m﹣1的函数值等于0
D.m﹣1的函数值与0的大小关系不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(5,﹣3)所在的象限是___________
相关试题

