【题目】连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( )
A.
B.
C.
D.
参考答案:
【答案】C
【解析】解: 连接BC,则BC为这个几何图形的直径,过O作OM⊥BC于M,
∵OB=OC,
∴∠BOM= ![]() ∠BOC=60°,
∠BOC=60°,
∴∠OBM=30°,
∵OB=2,OM⊥BC,
∴OM= ![]() OB=1,由勾股定理得:BM=
OB=1,由勾股定理得:BM= ![]() ,
,
∴由垂径定理得:BC=2 ![]() ;
;
连接AC、BD,
则BD为这个图形的直径,
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC,
∵∠ABC=60°,
∴∠ABO=30°,
∴AO= ![]() AB=1,由勾股定理得:BO=
AB=1,由勾股定理得:BO= ![]() ,
,
∴BD=2BO=2 ![]() ;
;
连接BD,
则BD为这个图形的直径,
由勾股定理得:BD= ![]() =2
=2 ![]() ;
;
连接BD,
则BD为这个图形的直径,
由勾股定理得:BD= ![]() =
= ![]() ,
,
∵2 ![]() >
> ![]() >2
>2 ![]() ,
,
∴选项A、B、D错误,选项C正确;
故选C.
【考点精析】本题主要考查了勾股定理的概念和菱形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.

(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有长度分别为2cm,3cm,4cm,7cm的四条线段,任取其中三条能组成三角形的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.

-
科目: 来源: 题型:
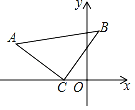
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点A的坐标为(﹣6,3),求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣
 x2﹣3x﹣
x2﹣3x﹣  ,设自变量的值分别为x1 , x2 , x3 , 且﹣3<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系是( )
,设自变量的值分别为x1 , x2 , x3 , 且﹣3<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系是( )
A.y1>y2>y3
B.y1<y2<y3
C.y2>y3>y1
D.y2<y3<y1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.

相关试题

