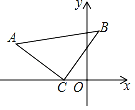
【题目】如图，在△ACB中，∠ACB=90°，AC=BC，点C的坐标为（﹣2，0），点A的坐标为（﹣6，3），求点B的坐标．

参考答案：

【答案】（1，4）.

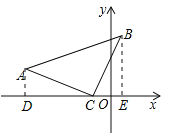
【解析】试题分析：过A和B分别作AD⊥OC于D，BE⊥OC于E，利用已知条件可证明△ADC≌△CEB，再由全等三角形的性质和已知数据即可求出B点的坐标．

试题解析：解：过A和B分别作AD⊥OC于D，BE⊥OC于E，∵∠ACB=90°，∴∠ACD+∠CAD=90°∠ACD+∠BCE=90°，∴∠CAD=∠BCE，在△ADC和△CEB中，∵∠ADC=∠CBE=90°，∠CAD=∠BCE，AC=BC，∴△ADC≌△CEB（AAS），∴DC=BE，AD=CE，∵点C的坐标为（﹣2，0），点A的坐标为（﹣6，3），∴OC=2，AD=CE=3，OD=6，∴CD=OD﹣OC=4，OE=CE﹣OC=3﹣2=1，∴BE=4，∴则B点的坐标是（1，4）．

关闭