【题目】如图,CD∥AB,∠ABC,∠BCD 的角平分线交 AD 于 E 点,且 E 在 AD 上,CE 交 BA 的延长线于 F 点.
(1)试问 BE 与 CF 互相垂直吗?若垂直,请说明理由;
(2)若 CD=3,AB=4,求 BC 的长 .
参考答案:
【答案】
(1)解:垂直,理由如下:
∵CD∥AB,
∴∠ABC+∠BCD=180°,
又∵∠ABC,∠BCD的角平分线交于E点,
∴∠ABE=∠EBC,∠DCE=∠ECB,
∴∠EBC+∠ECB=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=90°,
(∠ABC+∠BCD)=90°,
∴∠CEB=90°,
∴BE 与 CF 互相垂直.
(2)解:由(1)知∠CEB=90°,
∴∠FEB=90°,
在△FBE 和△CBE 中,
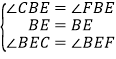
∴△FBE≌△CBE(ASA),
∴BF=BC,EF=EC,
又∵CD∥AB,
∴∠DCE=∠AFE,
在△DCE和△AFE中,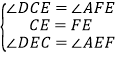
∴△DCE≌△AFE,
∴DC=AF,
∵CD=3,AB=4,
∴BC=BF=AF+AB=CD+AB=3+4=7,
【解析】(1)垂直,理由如下:由两直线平行,同旁内角互补得出∠ABC+∠BCD=180°;又由角平分线定义得出∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD,
∠BCD,
从而得出∠EBC+∠ECB=90°,根据三角形内角和定理得出∠CEB=90°,即BE 与 CF 互相垂直.
(2)由(1)知∠CEB=∠FEB=90°,根据ASA得△FBE≌△CBE,再由全等三角形的性质得出BF=BC,EF=EC;又由两直线平行,内错角相等,得到∠DCE=∠AFE,由ASA得△DCE≌△AFE,再根据全等三角形的性质得出DC=AF,由已知条件和等量代换求出BC的值.
【考点精析】关于本题考查的角的平分线和平行线的性质,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】折纸的思考.
【操作体验】
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片
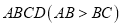 (图①),使
(图①),使 与
与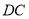 重合,得到折痕
重合,得到折痕 ,把纸片展平(图②).
,把纸片展平(图②).第二步,如图③,再一次折叠纸片,使点
 落在
落在 上的
上的 处,并使折痕经过点
处,并使折痕经过点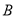 ,得到折痕
,得到折痕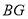 ,折出
,折出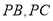 ,得到
,得到 .
.(1)说明
 是等边三角形.
是等边三角形.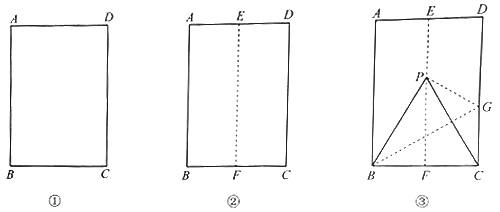
【数学思考】
(2)如图④.小明画出了图③的矩形
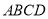 和等边三角形
和等边三角形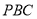 .他发现,在矩形
.他发现,在矩形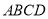 中把
中把 经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.
经过图形变化,可以得到图⑤中的更大的等边三角形.请描述图形变化的过程.(3)已知矩形一边长为3
 ,另一边长为
,另一边长为 .对于每一个确定的
.对于每一个确定的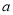 的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的
的值,在矩形中都能画出最大的等边三角形.请画出不同情形的示意图,并写出对应的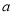 的取值范围.
的取值范围.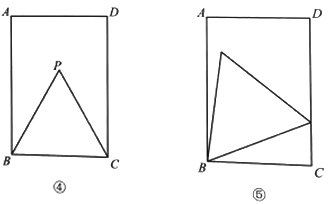
【问题解决】
(4)用一张正方形铁片剪一个直角边长分别为4
 和1
和1 的直角三角形铁片,所需正方形铁片的边长的最小值为
的直角三角形铁片,所需正方形铁片的边长的最小值为  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个数的立方根就是它本身,则这个数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为常数)
为常数)(1)该函数的图像与
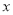 轴公共点的个数是( )
轴公共点的个数是( )A.0 B.1 C.2 D.1或2
(2)求证:不论
 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数 的图像上.
的图像上.(3)当
 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在以下列三个数为边长的三角形中,不能组成直角三角形的是( )
A. 4、7、9 B. 5、12、13 C. 6、8、10 D. 7、24、25
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(x3)2=x5
B.(﹣x)5=﹣x5
C.x3x2=x6
D.3x2+2x3=5x5
相关试题

