【题目】如图,过矩形![]() 的对角线
的对角线![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() ,交
,交![]() 边于点
边于点![]() ,分别连接
,分别连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )

A. ![]() B. 4C.
B. 4C. ![]() D. 6
D. 6
参考答案:
【答案】B
【解析】
求出∠ACB=∠DAC,然后利用“角角边”证明△AOF和△COE全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相垂直平分的四边形是菱形得到四边形AECF是菱形,再求出∠ECF=60°,然后判断出△CEF是等边三角形,根据等边三角形的三条边都相等可得EF=CF,根据矩形的对边相等可得CD=AB,然后求出CF,从而得解.
∵矩形对边AD∥BC,
∴∠ACB=∠DAC,
∵O是AC的中点,
∴AO=CO,
在△AOF和△COE中,
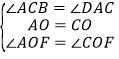 ,
,
∴△AOF≌△COE(ASA),
∴OE=OF,
又∵EF⊥AC,
∴四边形AECF是菱形,
∵∠DCF=30°,
∴∠ECF=90°-30°=60°,
∴△CEF是等边三角形,
∴EF=CF,
∵AB=![]() ,
,
∴CD=AB=![]() ,
,
∵∠DCF=30°,
∴DF=![]() ,
,
∴CF2=DF2+CD2,即![]() ,
,
∴CF=4,
∴EF=4.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
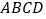 中,点
中,点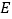 是
是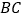 边上的一动点,点
边上的一动点,点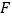 是
是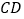 上一点,且
上一点,且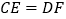 ,
,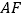 、
、 相交于点
相交于点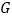 .
.(1)求证:
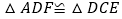 ;
;(2)求
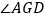 的度数
的度数(3)若
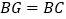 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货11吨;用1辆A型车和2辆B型车载满货物一次可运货13吨.根据以上信息, 解答下列问题:
(1)1辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物,计划同时租用A型车
 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都载满货物请用含有
辆,一次运完,且恰好每辆车都载满货物请用含有 的式子表示
的式子表示 ,并帮该物流公司设计租车方案;
,并帮该物流公司设计租车方案;(3)在(2)的条件下,若A型车每辆需租金500元/次,B型车每辆需租金600元/次.请选出最省钱的租车方案,并求出最少租车费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
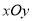 中,抛物线
中,抛物线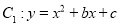 经过点
经过点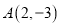 ,且与
,且与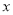 轴的一个交点为
轴的一个交点为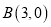 .
.(1)求抛物线
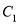 的表达式;
的表达式;(2)
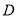 是抛物线
是抛物线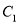 与
与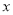 轴的另一个交点,点
轴的另一个交点,点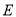 的坐标为
的坐标为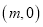 ,其中
,其中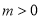 ,△
,△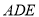 的面积为
的面积为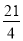 .
.①求
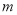 的值;
的值;②将抛物线
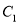 向上平移
向上平移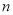 个单位,得到抛物线
个单位,得到抛物线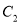 .若当
.若当 时,抛物线
时,抛物线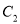 与
与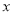 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
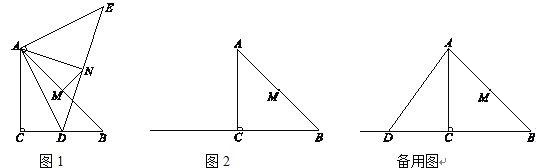
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC=4,M为AB的中点.D是射线BC上一个动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED,N为ED的中点,连接AN,MN.
(1)如图1,当BD=2时,AN=___ __,NM与AB的位置关系是____ _____;
(2)当4<BD<8时,
①依题意补全图2;
②判断(1)中NM与AB的位置关系是否发生变化,并证明你的结论;
(3)连接ME,在点D运动的过程中,当BD的长为何值时,ME的长最小?最小值是多少?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 、
、 分别是正方形
分别是正方形 的边
的边 、
、 上的点,且
上的点,且 ,
, 、
、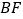 相交于点
相交于点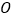 ,下列结论:①
,下列结论:① ;②
;② ;③
;③ ,其中一定正确的有( )
,其中一定正确的有( )
A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
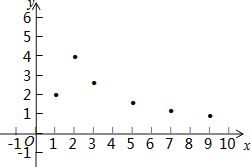
查看答案和解析>>【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:

小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为_____________;
②该函数的一条性质:_____________.
相关试题

