【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,且与
,且与![]() 轴的一个交点为
轴的一个交点为![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)![]() 是抛物线
是抛物线![]() 与
与![]() 轴的另一个交点,点
轴的另一个交点,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() ,△
,△![]() 的面积为
的面积为![]() .
.
①求![]() 的值;
的值;
②将抛物线![]() 向上平移
向上平移![]() 个单位,得到抛物线
个单位,得到抛物线![]() .若当
.若当![]() 时,抛物线
时,抛物线![]() 与
与![]() 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②答案见解析.
;②答案见解析.
【解析】试题分析:(1)将A、B的坐标代入抛物线解析式求出b、c即可;(2)①过A作AF⊥x轴与点F,如图1,首先求出D的坐标,再根据△ADE的面积可求出DE的长度,接着可求出OE的长度即m的值;②利用抛物线的平移变换,可设抛物线C2的表达式为y=(x-1)2-4+n,接下去分类讨论:求出抛物线过点E和过原点时对应的n的值,并画出图像,利用图像可确定n的范围;当抛物线顶点再x轴上时,求出n的值.综上得到n的取值范围.
试题解析:
(1)∵抛物线C1:y=x2+bx+c经过点A(2,-3),且与x轴的一个交点为B(3,0),
∴![]() ,
,
解得![]() ,
,
∴抛物线C1解析式为y=x2-2x-3;
(2)
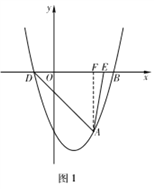
①过A作AF⊥x轴与点F,如图1,
∵y=x2-2x-3=(x-1)2-4,
∴抛物线对称轴为:x=1,
∴D(-1,0),
∵E(m,0),m>0,
∴S△ADE=![]() DE·AF=
DE·AF=![]() DE×3=
DE×3=![]() ,
,
∴DE=![]() ,
,
∴m=OE=DE-OD=![]() .
.
②
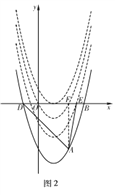
设抛物线C2的表达式为y=(x-1)2-4+n,
如图2,当抛物线C2经过E(![]() ,0)时,
,0)时,
(![]() -1)2-4+n=0,解得n=
-1)2-4+n=0,解得n=![]() ;
;
当抛物线C2经过原点时,
(0-1)2-4+n=0,解得n=3;
∵0≤x≤![]() 时,抛物线C2与x轴只有一个公共点,
时,抛物线C2与x轴只有一个公共点,
∴结合图像可知,当![]() ≤n<3时,符合题意.
≤n<3时,符合题意.
令y=0,(x-1)2-4+n=0,
由题意得,b2-4ac=16-4n=0,解得n=4.
综上, ![]() ≤n<3或n=4.
≤n<3或n=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形 ABCD 绕点 A 按逆时针方向旋转到正方形AB ' C ' D ' ,旋转角为 ( 0<< 180 ) ,连接 B ' D 、 C ' D ,若 B ' D C ' D ,则 =____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,点
中,点 是
是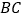 边上的一动点,点
边上的一动点,点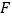 是
是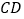 上一点,且
上一点,且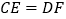 ,
,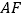 、
、 相交于点
相交于点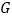 .
.(1)求证:
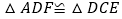 ;
;(2)求
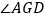 的度数
的度数(3)若
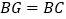 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货11吨;用1辆A型车和2辆B型车载满货物一次可运货13吨.根据以上信息, 解答下列问题:
(1)1辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物,计划同时租用A型车
 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都载满货物请用含有
辆,一次运完,且恰好每辆车都载满货物请用含有 的式子表示
的式子表示 ,并帮该物流公司设计租车方案;
,并帮该物流公司设计租车方案;(3)在(2)的条件下,若A型车每辆需租金500元/次,B型车每辆需租金600元/次.请选出最省钱的租车方案,并求出最少租车费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过矩形
 的对角线
的对角线 的中点
的中点 作
作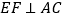 ,交
,交 边于点
边于点 ,交
,交 边于点
边于点 ,分别连接
,分别连接 、
、 ,若
,若 ,
, ,则
,则 的长为( )
的长为( )
A.
 B. 4C.
B. 4C.  D. 6
D. 6 -
科目: 来源: 题型:
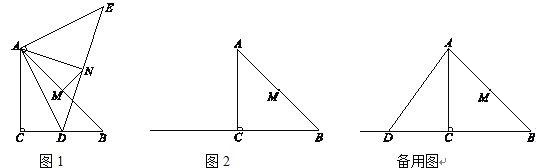
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC=4,M为AB的中点.D是射线BC上一个动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED,N为ED的中点,连接AN,MN.
(1)如图1,当BD=2时,AN=___ __,NM与AB的位置关系是____ _____;
(2)当4<BD<8时,
①依题意补全图2;
②判断(1)中NM与AB的位置关系是否发生变化,并证明你的结论;
(3)连接ME,在点D运动的过程中,当BD的长为何值时,ME的长最小?最小值是多少?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 、
、 分别是正方形
分别是正方形 的边
的边 、
、 上的点,且
上的点,且 ,
, 、
、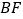 相交于点
相交于点 ,下列结论:①
,下列结论:① ;②
;② ;③
;③ ,其中一定正确的有( )
,其中一定正确的有( )
A. 0个B. 1个C. 2个D. 3个
相关试题

