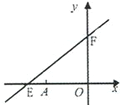
【题目】如图,直线y=kx+6与x轴、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为9,并说明理由.
参考答案:
【答案】(1)![]() ;(2)S
;(2)S![]() x+18 (-8<x<0);(3)(-4,3).
x+18 (-8<x<0);(3)(-4,3).
【解析】
(1)将点E坐标(﹣8,0)代入直线y=kx+6就可以求出k值;
(2)先求出函数的解析式,再由点A的坐标为(﹣6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)根据△OPA的面积为9代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
(1)∵点E(﹣8,0)在直线y=kx+6上,∴0=﹣8k+6,∴k![]() ;
;
(2)∵k![]() ,∴直线的解析式为:y
,∴直线的解析式为:y![]() x+6.
x+6.
∵P点在y![]() x+6上,设P(x,
x+6上,设P(x,![]() x+6),∴△OPA以OA为底的边上的高是|
x+6),∴△OPA以OA为底的边上的高是|![]() x+6|,当点P在第二象限时,|
x+6|,当点P在第二象限时,|![]() x+6|
x+6|![]() x+6.
x+6.
∵点A的坐标为(﹣6,0),∴OA=6,∴S![]() x+18.
x+18.
∵P点在第二象限,∴﹣8<x<0;∴S![]() x+18 (-8<x<0);
x+18 (-8<x<0);
(3)设点P(x,y)时,其面积S![]() 9,则
9,则![]() x+18=9,解得:x=-4.
x+18=9,解得:x=-4.
∵P点在y![]() x+6上,∴y
x+6上,∴y![]() ×(-4)+6=3,故P(-4,3).
×(-4)+6=3,故P(-4,3).
所以,P(-4,3)时,三角形OPA的面积为9.
-
科目: 来源: 题型:
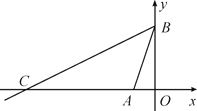
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C两点,且∠CBA=45° 求直线BC的解析式.
-
科目: 来源: 题型:
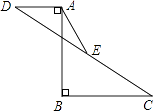
查看答案和解析>>【题目】如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )
A.6
B.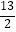
C.5
D.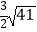
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向点B以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动;如果同时出发,则过3秒时,求△BPQ的面积。

-
科目: 来源: 题型:
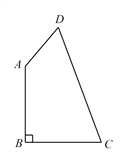
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿直线AD折叠,点B与点E重合,连接BE交AD于O.∠ABC=90°,AB=6,BC=8,AC=10,SACD=15.有下列结论:①SCDE=5;②CD=5;③OB=OE;④SABD:SACD=3:4,则以上结论正确的是( )
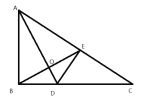
A. ①②B. ②③C. ②③④D. ①②③
相关试题

