【题目】如图,半径为2的圆被分成甲、乙、丙三个扇形,它们的面积之比为3:2:5.请回答下列问题.
(1)扇形甲的圆心角为 ;
(2)剪下扇形丙恰好能围成一个几何体的侧面,这个几何体的名称是 .
(3)现有半径分别为1,2,3的三个圆形纸片,从中选择一个恰好和扇形丙组成(2)中的几何体(不考虑接缝的大小),求这个几何体的表面积.

参考答案:
【答案】(1)108°;(2)圆锥;(3)3π.
【解析】
(1)根据扇形的面积比等于圆心角之比,求出各个扇形的圆心角占整个圆的几分之几,进而确定出各个扇形的圆心角;
(2)根据圆锥的侧面展开图形为扇形,进行解答便可;
(3)由圆锥侧面展开图扇形的弧长与圆锥底面圆周长相等,便可选择底面圆,根据圆锥表面积公式进行计算.
解:(1)360°×![]() =108°,
=108°,
故答案为:108°;
(2)∵一个扇形可以转成一个圆锥的侧面,
∴剪下扇形丙恰好能围成一个几何体的侧面,这个几何体的名称是圆锥,
故答案为:圆锥;
(3)扇形丙的圆心角为:360°×![]() ,
,
设剪下扇形丙能围成圆锥的底面圆的半径为x,根据题意得,
2πx=![]() ,
,
∴x=1,
∴选择半径为1的圆形纸片恰好和扇形丙组成(2)中的几何体;
该几何体的表面积为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )
A.3平方千米B.7.5平方千米C.15平方千米D.30平方千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
 ,
, ,
, ,
, ,…,则第8个等式是__________.
,…,则第8个等式是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)写出点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;
(3)点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①
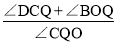 的值不变;②
的值不变;②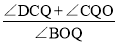 的值不变,其中有且只有一个正确,请你找出这个结论并求值.
的值不变,其中有且只有一个正确,请你找出这个结论并求值.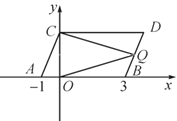
-
科目: 来源: 题型:
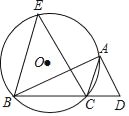
查看答案和解析>>【题目】如图,点B,C为⊙O上一动点,过点B作BE∥AC,交⊙O于点E,点D为射线BC上一动点,且AC平分∠BAD,连接CE.
(1)求证:AD∥EC;
(2)连接EA,若BC=6,则当CD= 时,四边形EBCA是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,过点P作PD⊥OP交圆O于点D.

(1)如图1,当PD∥AB 时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上小明用一副三角板进行如下操作:把一副三角板中两个直角的顶点重合,一个三角板固定不动,另一个三角板绕着重合的顶点旋转(两个三角板始终有重合部分).
(1)当旋转到如图所示的位置时,量出∠α=25°,通过计算得出∠AOD=∠BOC= ;
(2)通过几次操作小明发现,∠α≠25°时.∠AOD=∠BOC仍然成立,请你帮他完成下面的说理过程.
理由:因为∠AOC=∠BOD= ;
所以,根据等式的基本性质∠ ﹣∠COD=∠BOD﹣∠ ;
即∠AOD=∠ .
(3)小莹还发现在旋转过程中∠AOB和∠DOC之间存在一个不变的数量关系,请你用等式表示这个数量关系 .

相关试题

