Question

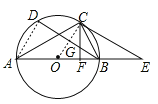
【题目】如图所示，以△ABC的边AB为直径作⊙O，点C在⊙O上，BD是⊙O的弦，∠A=∠CBD，过点C作CF⊥AB于点F，交BD于点G，过C作CE∥BD交AB的延长线于点E．

（1）求证：CE是⊙O的切线；

（2）求证：CG=BG；

（3）若∠DBA=30°，CG=4，求BE的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）．

【解析】试题分析：（1）连接OC，先证得，根据垂径定理得到OC⊥BD，根据CE∥BD推出OC⊥CE，即可得到结论；

（2）根据圆周角定理得出∠ACB=90°，然后根据同角的余角相等得出∠A=∠BCF，即可证得∠BCF=∠CBD，根据同角对等边即可证得结论；

（3）连接AD，根据圆周角定理得出∠ADB=90°，即可求得∠BAD=60°，根据圆周角定理得出∠DAC=∠BAC=30°，解直角三角形求得=tan30°=，然后根据三角形相似和等腰三角形的判定即可求得BE的值．

（1）证明：连接OC，∵∠A=∠CBD，∴ ，∴OC⊥BD，∵CE∥BD，∴OC⊥CE，∴CE是⊙O的切线；

（2）证明：∵AB为直径，∴∠ACB=90°，∵CF⊥AB，∴∠ACB=∠CFB=90°，∵∠ABC=∠CBF，∴∠A=∠BCF，∵∠A=∠CBD，∴∠BCF=∠CBD，∴CG=BG；

（3）解：连接AD，∵AB为直径，∴∠ADB=90°，∵∠DBA=30°，∴∠BAD=60°，∵，∴∠DAC=∠BAC=∠BAD=30°，∴=tan30°=，∵CE∥BD，∴∠E=∠DBA=30°，∴AC=CE，∴ =，∵∠A=∠BCF=∠CBD=30°，∴∠BCE=30°，∴BE=BC，∴△CGB∽△CBE，∴ ==，∵CG=4，∴BC=，∴BE=．