【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
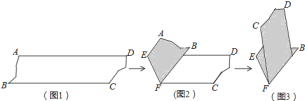
A.120°B.108°C.126°D.114°
参考答案:
【答案】D
【解析】
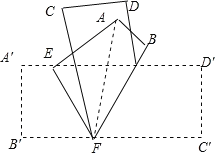
如图,设∠B′FE=x,根据折叠的性质得∠BFE=∠B′FE=x,∠AEF=∠A′EF,则∠BFC=x-18°,再由第2次折叠得到∠C′FB=∠BFC=x-18°,于是利用平角定义可计算出x=66°,接着根据平行线的性质得∠A′EF=180°-∠B′FE=114°,所以∠AEF=114°.
如图,设∠B′FE=x,
∵纸条沿EF折叠,
∴∠BFE=∠B′FE=x,∠AEF=∠A′EF,
∴∠BFC=∠BFE∠CFE=x18°,
∵纸条沿BF折叠,
∴∠C′FB=∠BFC=x18°,
而∠B′FE+∠BFE+∠C′FB=180°,
∴x+x+x18°=180°,解得x=66°,
∵A′D′∥B′C′,
∴∠A′EF=180°∠B′FE=180°66°=114°,
∴∠AEF=114°.
故答案选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是( )
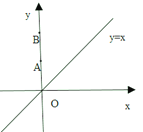
A. 6B. 5C. 4D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:

(2)计算:(2+
 )(2﹣
)(2﹣ )+
)+ ÷
÷ +
+
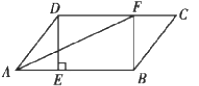
(3)在ABCD中,过点D作DE⊥AB于点E,点F在CD上且DF=BE,连接AF,BF.
①求证:四边形BFDE是矩形;
②若CF=6,BF=8,AF平分∠DAB,则DF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(知识背景)在学习计算框图时,可以用
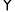 表示数据输入、输出框;
表示数据输入、输出框; 用表示数据处理和运算框:用◇表示数据判断框(根据条件决定执行两条路径中的某一条)
用表示数据处理和运算框:用◇表示数据判断框(根据条件决定执行两条路径中的某一条)(尝试解决)
(1)①如图1,当输入数
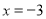 时,输出数y=_________;
时,输出数y=_________;②如图2,第一个“
 ”内,应填_________;第二个“
”内,应填_________;第二个“ ”内,应填_________;
”内,应填_________;(2)①如图3,当输入数
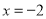 时,输出数
时,输出数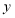 =_________;
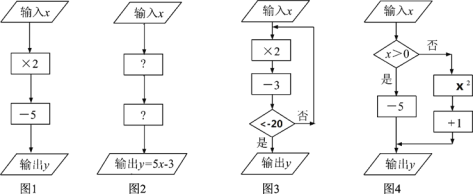
=_________;②如图4,当输出的值
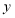 =26,则输入的值
=26,则输入的值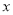 =_________;
=_________;
(实际应用)
(3)为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量
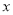 ,输出数为水费
,输出数为水费 .
. -
科目: 来源: 题型:
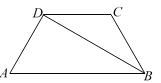
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
求:(1)求∠CDB的度数;
(2)当AD=2时,求对角线BD的长和梯形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张明、王成两位同学在初二学年10次数学单元检测的成绩(成绩均为整数,且个位数为0)如图所示利用图中提供的信息,解答下列问题:
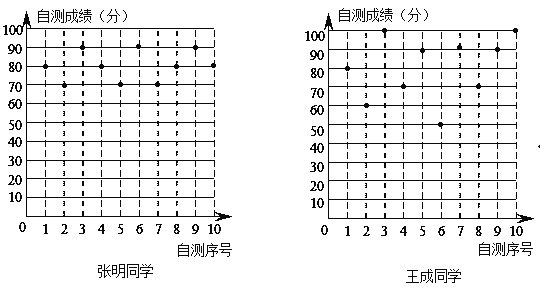
(1)完成下表:
姓名
平均成绩
中位数
众数
方差(s2)
张明
80
80
王成
260
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率较高的同学是 ;
(3)根据图表信息,请你对这两位同学各提出学习建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C三地在同一条路上,A地在B地的正南方3千米处,甲、乙两人分别从A、B两地向正北方向的目的地C匀速直行,他们分别和A地的距离s(千米)与所用的时间t(小时)的函数关系如图所示.

(1)图中的线段l1是 (填“甲”或“乙”)的函数图象,C地在B地的正北方向 千米处;
(2)谁先到达C地?并求出甲乙两人到达C地的时间差;
(3)如果速度慢的人在两人相遇后立刻提速,并且比先到者晚1小时到达C地,求他提速后的速度.
相关试题

