【题目】已知A、B、C三地在同一条路上,A地在B地的正南方3千米处,甲、乙两人分别从A、B两地向正北方向的目的地C匀速直行,他们分别和A地的距离s(千米)与所用的时间t(小时)的函数关系如图所示.

(1)图中的线段l1是 (填“甲”或“乙”)的函数图象,C地在B地的正北方向 千米处;
(2)谁先到达C地?并求出甲乙两人到达C地的时间差;
(3)如果速度慢的人在两人相遇后立刻提速,并且比先到者晚1小时到达C地,求他提速后的速度.
参考答案:
【答案】(1)乙;3;(2)甲先到达,到达目的地的时间差为![]() 小时;(3)速度慢的人提速后的速度为
小时;(3)速度慢的人提速后的速度为![]() 千米/小时.
千米/小时.
【解析】分析:
(1)根据题意结合所给函数图象进行判断即可;
(2)由所给函数图象中的信息先求出二人所对应的函数解析式,再由解析式结合图中信息求出二人到达C地的时间并进行比较、判断即可得到本问答案;
(3)根据图象中的信息结合(2)中的结论进行解答即可.
详解:
(1)由题意结合图象中的信息可知:图中线段l1是乙的图象;C地在B地的正北方6-3=3(千米)处.
(2)甲先到达.
设甲的函数解析式为s=kt,则有4=t,
∴s=4t.
∴当s=6时,t=![]() .
.
设乙的函数解析式为s=nt+3,则有4=n+3,即n=1.
∴乙的函数解析式为s=t+3.
∴当s=6时,t=3.
∴甲、乙到达目的地的时间差为:![]() (小时).
(小时).
(3)设提速后乙的速度为v千米/小时,
∵相遇处距离A地4千米,而C地距A地6千米,
∴相遇后需行2千米.
又∵原来相遇后乙行2小时才到达C地,
∴乙提速后2千米应用时1.5小时.
即![]() ,解得:
,解得:![]() ,
,
答:速度慢的人提速后的速度为![]() 千米/小时.
千米/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
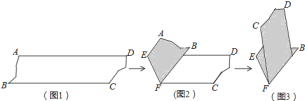
A.120°B.108°C.126°D.114°
-
科目: 来源: 题型:
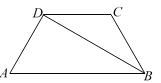
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
求:(1)求∠CDB的度数;
(2)当AD=2时,求对角线BD的长和梯形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张明、王成两位同学在初二学年10次数学单元检测的成绩(成绩均为整数,且个位数为0)如图所示利用图中提供的信息,解答下列问题:
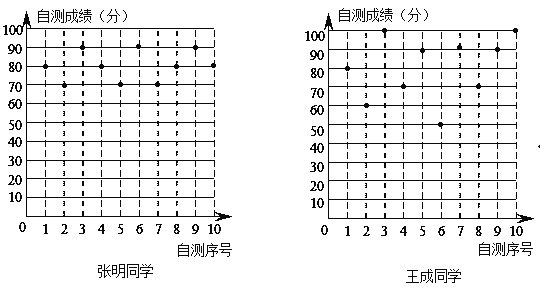
(1)完成下表:
姓名
平均成绩
中位数
众数
方差(s2)
张明
80
80
王成
260
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率较高的同学是 ;
(3)根据图表信息,请你对这两位同学各提出学习建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)
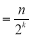 (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN.

(1)求证:四边形ENFM为平行四边形;
(2)当四边形ENFM为矩形时,求证:BE=BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
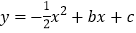 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
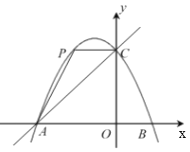
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
相关试题

