【题目】如图,在直角坐标系平面内,函数y=![]() (x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(1)求反比例函数解析式;
(2)当△ABD的面积为S,试用a的代数式表示求S.
(3)当△ABD的面积为2时,判断四边形ABCD的形状,并说明理由.

参考答案:
【答案】(1)反比例函数解析式为y=![]() ;(2)S=2a﹣2;(3)四边形ABCD为菱形,理由见解析.
;(2)S=2a﹣2;(3)四边形ABCD为菱形,理由见解析.
【解析】试题分析:(1)把A(1,4)代入y=![]() ,用待定系数法求解即可;
,用待定系数法求解即可;
(2)把B(a,b)代入(1)中求得解析式中,求出b与a的关系,根据三角形的面积公式列式即可;
(3)把S=2代入(2)中的解析式中,求出a的值,可知四边形ABCD的对角线互相垂直平分,从而可证明四边形ABCD为菱形.
解:(1)把A(1,4)代入y=![]() 得m=1×4=4,
得m=1×4=4,
所以反比例函数解析式为y=![]() ;
;
(2)把B(a,b)代入y=![]() 得b=
得b=![]() ,
,
所以S=![]() a(4﹣
a(4﹣![]() )=2a﹣2;
)=2a﹣2;
(3)四边形ABCD为菱形.理由如下:
当S=2时,2a﹣2=2,解得a=2,
所以AC与BD互相垂直平分,
所以四边形ABCD为菱形.
-
科目: 来源: 题型:
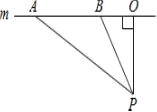
查看答案和解析>>【题目】随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点P,在笔直的车道m上确定点O,使PO和m垂直,测得PO的长等于21米,在m上的同侧取点A、B,使∠PAO=30°,∠PBO=60°.
(1)求A、B之间的路程(保留根号);
(2)已知本路段对校车限速为12米/秒若测得某校车从A到B用了2秒,这辆校车是否超速?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图中提供的信息,回答下列问题:

(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和n(n>10,且n为整数)个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为两人对抗赛,即把四种比赛项目写在4张完全相同的卡片上,比赛时,比赛的两人从中随机抽取1张卡片作为自己的比赛项目(不放回,且每人只能抽取一次)比赛时,小红和小明分到一组.(1)小明先抽取,那么小明抽到唐诗的概率是多少?
(2)小红擅长唐诗,小红想:“小明先抽取,我后抽取”抽到唐诗的概率是不同的,且小明抽到唐诗的概率更大,若小红后抽取,小红抽中唐诗的概率是多少?小红的想法对吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=150°,OC为∠AOB内部的一条射线,∠BOC=60°.
(1)如图1,若OE平分∠AOB,OD为∠BOC内部的一条射线,∠COD=
 ∠BOD,求∠DOE的度数;
∠BOD,求∠DOE的度数;(2)如图2,若射线OE绕着O点从OA开始以15度/秒的速度顺时针旋转至OB结束、OF绕着O点从OB开始以5度秒的速度逆时针旋转至OA结束,运动时间为t秒,当∠EOC=∠FOC时,求t的值:
(3)若射线OM绕着O点从OA开始以15度秒的速度逆时针旋转至OB结束,在旋转过程中,ON平分∠AOM,试问2∠BON一∠BOM在某时间段内是否为定值,若不是,请说明理由;若是请补全图形,求出这个定值并写出t所在的时间段.(本题中的角均为大于0°且小于180°的角)

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|﹣2|+|﹣10|﹣|﹣5|
(2)(﹣3.5)+(+8
 )﹣(﹣5.5)+(﹣2
)﹣(﹣5.5)+(﹣2 )
)(3)﹣42+3×(﹣2)2×(
 -1)÷(﹣1
-1)÷(﹣1 )
)(4)(
 ﹣
﹣ ﹣
﹣ )×(﹣24)+42÷(﹣2)3+(﹣1)2019
)×(﹣24)+42÷(﹣2)3+(﹣1)2019 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段a,b,∠α(如图).
(1)以线段a,b为一组邻边作平行四边形,这样的平行四边形能作____个.
(2)以线段a,b为一组邻边,它们的夹角为∠α,作平行四边形,这样的平行四边形能作_____个,作出满足条件的平行四边形(要求仅用直尺和圆规,保留作图痕迹,不写做法)

相关试题

