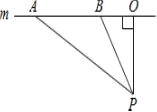
【题目】随着近几年我市私家车日越增多，超速行驶成为引发交通事故的主要原因之一．某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动，设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点P，在笔直的车道m上确定点O，使PO和m垂直，测得PO的长等于21米，在m上的同侧取点A、B，使∠PAO=30°，∠PBO=60°．

（1）求A、B之间的路程（保留根号）；

（2）已知本路段对校车限速为12米/秒若测得某校车从A到B用了2秒，这辆校车是否超速？请说明理由．

参考答案：

【答案】（1）AB=14米；（2）这辆校车超速；理由见解析.

【解析】试题分析：（1）Rt△OPC与Rt△BOP中，先根据锐角三角函数的定义求出AO及BO的长，再根据AB=AO-BO即可得出结果；

（2）先根据汽车从A到B用时2秒求出其速度，再与已知相比较即可．

解：（1）在Rt△AOP中，∵PO=21米，∠PAO=30°，

∴AO===21（米）；

在Rt△BOP中，∵PO=21米，∠PBO=60°，

∴BO===7（米），

∴AB=AO﹣BO=14米；

（2）这辆校车超速；理由如下：

∵校车从A到B用时2秒，

∴速度为14÷2=7（米/秒）＞12米/秒，

∴这辆校车在AB路段超速．

关闭